
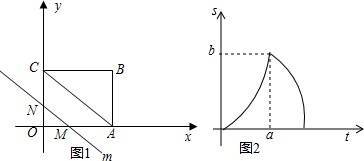
分析 (1)根据图象和矩形的面积公式进行解答;
(2)利用待定系数法和相似三角形的判定和性质得出0<t≤4和4<t<8的解析式即可;
(3)由矩形OABC的面积为12被分成1:3两部分分0<t≤4和4<t<8两种情况进行解答.
解答 解:(1)因为OA=4,OC=3,
所以可得点B的坐标为(4,3),
矩形的面积=4×3=12,
根据图象得出当a=4时,面积=$\frac{1}{2}×4×3=6$,即b=6,
故答案为:B(4,3),矩形OABC的面积=12,
a=4,b=6;
(2)当0<t≤4时,如图1,
∵MN∥AC,
∴$\frac{OM}{OA}=\frac{ON}{OC}$,即$\frac{t}{4}=\frac{ON}{3}$,
解得:ON=$\frac{3t}{4}$,
∴S=$\frac{1}{2}OM•ON=\frac{1}{2}t•\frac{3}{4}t=\frac{3}{8}{t}^{2}$,
当4<t<8时,如图2,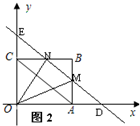
∵OD=t,
∴AD=t-4,
由△DAM∽△AOC,得AM=$\frac{3}{4}(t-4)$,
∴BM=$6-\frac{3}{4}t$,
由△BMN∽△BAC,得BN=$\frac{4}{3}BM$=8-t,
∴CN=t-4,
∴S=S矩形OABC-S△OAM-S△MBN-S△NCO
=12-$\frac{3}{2}(t-4)-\frac{1}{2}(8-t)(6-\frac{3}{4}t)-\frac{3}{2}(t-4)=-\frac{3}{8}{t}^{2}+3t$,
(另解:S=S△ODN-S△ODM=$\frac{3}{2}t-\frac{t-\frac{3}{4}(t-4)}{2}=-\frac{3}{8}{t}^{2}+3t$ )
(3)∵矩形OABC的面积为12被分成1:3两部分,
∴可得分成三角形和五边形的面积分别为3和9,
当0<t≤4时,S△AOC=3,
∴$\frac{3}{8}{t}^{2}=3$,
解得$t=2\sqrt{2}$,
当4<t<8时,S△MBN=3,
∴$\frac{1}{2}(8-t)(6-\frac{3}{4}t)$=3,
解得${t}_{1}=8-2\sqrt{2}$,${t}_{2}=8+2\sqrt{2}>8$(不合题意,舍去),
综上:当t=$2\sqrt{2}$或t=$8-2\sqrt{2}$时矩形OABC的面积被MN分成1:3两部分.
点评 此题考查相似三角形综合问题,关键是利用图象和相似三角形的判定和性质进行分析解答.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3种 | B. | 4种 | C. | 5种 | D. | 6种 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
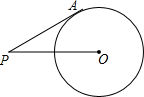 如图,P为⊙O外一点,PA切⊙O于点A,⊙O的半径为6,且PA=8,则cos∠APO等于( )
如图,P为⊙O外一点,PA切⊙O于点A,⊙O的半径为6,且PA=8,则cos∠APO等于( )| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com