
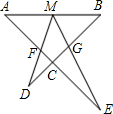
 如图,M为线段AB上一点,AE与BD交于点C,∠DME=∠A=∠B=α,且DM交AE于点F,ME交BD于点G.
如图,M为线段AB上一点,AE与BD交于点C,∠DME=∠A=∠B=α,且DM交AE于点F,ME交BD于点G.分析 (1)由∠AMF=∠B+∠D,∠BGM=∠DME+∠D,∠DME=∠A=∠B=α,可求得∠AMF=∠BGM,即可证得△AMF∽△BGM,然后由∠B是公共角,∠D是公共角,证得△AME∽△MFE,△BMD∽△MGD;
(2)由△AMF∽△BGM,根据相似三角形的对应边成比例,可得$\frac{FM}{GM}=\frac{AM}{BG}$,又由AM=BM,即可证得$\frac{FM}{GM}=\frac{BM}{BG}$,然后由∠DME=∠B,证得:△MFG∽△BMG;
(3)由α=45°,可得△ABC是等腰直角三角形,又由△AMF∽△BGM,可得$\frac{AM}{BG}=\frac{AF}{BM}$,即可求得BG的长,继而求得CF与CG的长,继而求得答案.
解答 (1)解:△AME∽△MFE,△BMD∽△MGD,△AMF∽△BGM,
理由:∵∠AMF=∠B+∠D,∠BGM=∠DME+∠D,
又∵∠DME=∠A=∠B=α,
∴∠AMF=∠BGM,
∴△AMF∽△BGM,
∵∠D是公共角,∠DME=∠B,
∴△BMD∽△MGD,
∵∠E是公共角,∠DME=∠A,
∴△AME∽△MFE;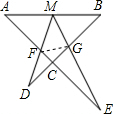 (2)证明:∵△AMF∽△BGM,
(2)证明:∵△AMF∽△BGM,
∴$\frac{FM}{GM}=\frac{AM}{BG}$,
∵AM=BM,
∴$\frac{FM}{GM}=\frac{BM}{BG}$,
即$\frac{FM}{BM}=\frac{GM}{BG}$,
∵∠DME=∠B,
∴△MFG∽△BMG;
(3)解:当α=45°时,可得AC⊥BC且AC=BC,
则AM=BM=2$\sqrt{2}$,
∵△AMF∽△BGM,
∴$\frac{AM}{BG}=\frac{AF}{BM}$,
∴BG=$\frac{AM•BM}{AF}$=$\frac{2\sqrt{2}•2\sqrt{2}}{3}$=$\frac{8}{3}$,AC=BC=4$\sqrt{2}$•cos45°=4,
∴CG=BC-BG=4-$\frac{8}{3}$=$\frac{4}{3}$,CF=AC-AF=4-3=1,
∴FG=$\sqrt{C{F}^{2}+C{G}^{2}}$=$\frac{5}{3}$.
点评 此题考查了相似三角形的判定与性质、等腰直角三角形的性质以及勾股定理.注意相似三角形的对应边成比例.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
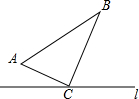 如图,△ABC中,∠ACB=90°,AC=6cm,BC=8cm,点P从A点出发沿A-C路径向终点C运动;点Q从B点出发沿B-C-A路径向终点A运动.点P和Q分别以每秒1cm和3cm的运动速度同时开始运动,其中一点到达终点时另一点也停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F.则点P运动时间为多少时,△PEC与△QFC全等?
如图,△ABC中,∠ACB=90°,AC=6cm,BC=8cm,点P从A点出发沿A-C路径向终点C运动;点Q从B点出发沿B-C-A路径向终点A运动.点P和Q分别以每秒1cm和3cm的运动速度同时开始运动,其中一点到达终点时另一点也停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F.则点P运动时间为多少时,△PEC与△QFC全等?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com