
分析 由规定的计算可知f(x)+f($\frac{1}{x}$)=1,由此分组求得答案,再相加即可求解.
解答 解:f(2015)+f(2014)+…+f(2)+f(1)+f($\frac{1}{2}$)+…+f($\frac{1}{2014}$)+f($\frac{1}{2015}$)
=[f(2015)+f($\frac{1}{2015}$)]+[f(2014)+f($\frac{1}{2014}$)]+…+[f(2)+f($\frac{1}{2}$)]+f(1)
=2014×1+$\frac{1}{1+1}$
=2014+$\frac{1}{2}$
=2014$\frac{1}{2}$.
故答案为:2014$\frac{1}{2}$.
点评 此题考查分式的加减法运算,掌握规定的运算方法,运算中找出规律,利用规律,解决问题.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:解答题
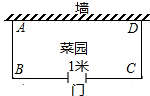 如图,用长为39米的篱笆(虚线部分),一面靠墙围成矩形ABCD菜园(AB<BC,且在边BC上开一个1米宽的门.要使围成的矩形ABCD菜园面积为128米2,那么矩形一边AB长应为多少米?
如图,用长为39米的篱笆(虚线部分),一面靠墙围成矩形ABCD菜园(AB<BC,且在边BC上开一个1米宽的门.要使围成的矩形ABCD菜园面积为128米2,那么矩形一边AB长应为多少米?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与C重合,再展开,折痕EF交AD边于E,交BC边于F,分别连接AF和CE,AE=10.
已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与C重合,再展开,折痕EF交AD边于E,交BC边于F,分别连接AF和CE,AE=10.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com