练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】方程9（x+1）2﹣4（x﹣1）2=0正确解法是（　　）

    A. 直接开方得3（x+1）=2（x﹣1）

    B. 化为一般形式13x2+5=0

    C. 分解因式得[3（x+1）+2（x﹣1）][3（x+1）﹣2（x﹣1）]=0

    D. 直接得x+1=0或x﹣l=0

    【答案】C

    【解析】

    根据方程的特点，应用平方差公式进行因式分解解方程即可.

    A：直接开平方应得到两个方程：3（x+1）=2（x-1）和3（x+1）=-2（x-1），所以A不正确；
    B：化成一般形式应是：5x2+26x+5=0；所以B不正确；
    C：方程左边满足平方差形式，可以用平方差公式因式分解为：[3（x+1）+2（x-1）][3（x+1）-2（x-1）]=0，所以C正确．
    D：两个完全平方的差为0，不能直接得到两个式子分别是0，只有两个完全平方的和是0，才能直接得到两个式子分别是0，所以D不对．
    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】若f(n)为n2+1(n为正整数的各位数字之和)，如：142+1＝197，1+9+7＝17，则f(14)＝17，记f1(n)＝f(n)，f2(n)＝f(f1(n))…，fk+1(n)＝f(fk(n))k为正整数，则f2008(8)＝______

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】用铝片做听装饮料瓶，现有100张铝片，每张铝片可制瓶身16个或瓶底45个，一个瓶身和两个瓶底可配成一套.用多少张制瓶身，多少张制瓶底可以正好制成配套的饮料瓶？设用x张铝片制瓶身，则可列方程为____________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校办工厂生产一批新产品，现有两种销售方案。

    方案一：在这学期开学时售出该批产品，可获利30000元，然后将该批产品的成本（生产该批产品支出的总费用）和已获利30000元进行再投资，到这学期结束时，再投资又可获利4.8%；

    方案二：这学期结束时售出该批产品，可获利35940元，但要付成本的0.2%作保管费。

    （1）设该批产品的成本为x元，方案一的获利为y1元，方案二的获利为y2元，分别求出y1，y2与x的关系式.

    （2）当该批产品的成本是多少元时，方案一与方案二的获利是一样的？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列关于x的一元二次方程中，有两个相等实数根的是（　　）

    A. x2＋1＝0 B. x2＋x﹣1＝0

    C. x2＋2x﹣3＝0 D. 4x2﹣4x＋1＝0

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有一条长40 cm的绳子，要把它围成一个矩形，若设矩形的一边长为x cm，回答以下问题：

    （1）怎样围成一个面积为75 cm的矩形？

    （2）能围成一个面积为101 cm的矩形吗？如能，说明围法；如不能，说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有两个一红一黄大小均匀的小正方体，每个小正方体的各个面上分别标有数字1，2，3，4，5，6.如同时掷出这两个小正方体，将它们朝上的面的数字分别组成一个两位数.（红色数字作为十位，黄色数字作为个位），请回答下列问题.

    （1）请分别写出一个必然事件和一个不可能事件.

    （2）得到的两位数可能有多少个？其中个位与十位上数字相同的有几个？

    （3）任写出一组两个可能性一样大的事件.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明投资销售一种进价为每件20元的护眼台灯．销售过程中发现，每月销售量y（件）与销售单价x（元）之间的关系可近似的看作一次函数：，在销售过程中销售单价不低于成本价，而每件的利润不高于成本价的80%．

    （1）设小明每月获得利润为w（元），求每月获得利润w（元）与销售单价x（元）之间的函数关系式，并确定自变量x的取值范围．

    （2）当销售单价定为多少元时，每月可获得最大利润？每月的最大利润是多少？

    （3）如果小明想要每月获得的利润为2000元，那么小明每月的成本需要多少元？（成本＝进价×销售量）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】观察下图，每个小正方形的边长均为1，可以得到每个小正方形的面积为1．

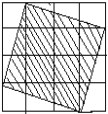
    （1）图中阴影部分的面积是多少？ 阴影部分正方形的边长是多少？

    （2）估计边长的值在哪两个整数之间？

    （3）请你利用图形在数轴上用刻度尺和圆规表示阴影部分正方形边长所表示的数。

    查看答案和解析>>

    同步练习册答案