
����Ŀ�����꼶�߰�����ѧ��ȤС�����Ժ����ĶԳƱ任����̽����������̽���������ù��̣��벹��������
(1)��������
��������y��|x|��ͼ��ʱ�������˷ֶκ����İ취���ú���ת��Ϊy��![]() ,������ͼ1��ʾ��ƽ��ֱ������ϵ������������ͼ����
,������ͼ1��ʾ��ƽ��ֱ������ϵ������������ͼ����
(2)���̽��
������y��|x��1|��ͼ����ת��Ϊ�ֶκ���y��![]() ��Ȼ��ֱ��������κ�����ͼ������С���������ƽ���ϵ���Գ�֪ʶ���Ѻ���y��x��1��x�����沿�֣���x����з��ۣ���x���ϼ����沿������˺���y��|x��1|��ͼ����ͼ2��ʾ��
��Ȼ��ֱ��������κ�����ͼ������С���������ƽ���ϵ���Գ�֪ʶ���Ѻ���y��x��1��x�����沿�֣���x����з��ۣ���x���ϼ����沿������˺���y��|x��1|��ͼ����ͼ2��ʾ��
(3)��չ���
��ͼ3�Ǻ���y��x2��2x��3��ͼ������ԭƽ��ֱ������ϵ������y��|x2��2x��3|��ͼ����
(4)ʵ������
�ٺ���y��|x2��2x��3|��ͼ����x���� �����㣬��Ӧ����|x2��2x��3|��0�� ��ʵ����
�ں���y��|x2��2x��3|��ͼ����ֱ��y��5�� �����㣬��Ӧ����|x2��2x��3|��5�� ��ʵ����
�ۺ���y��|x2��2x��3|��ͼ����ֱ��y��4�� �����㣬��Ӧ����|x2��2x��3|��4�� ��ʵ����
�ܹ���x�ķ���|x2��2x��3|��a��4��ʵ��ʱ��a��ȡֵ��Χ�� ��

���𰸡�(1)��ͼ�������� (3) ��ͼ������;
(4)��2��2����2��2����3,3����0��a��4��
����������������� ![]() ������㷨��
������㷨��![]() ��ͼ��
��ͼ��
![]() ���ݾ���ֵ�����壬���÷������۵�˼��д���ֶκ�����
���ݾ���ֵ�����壬���÷������۵�˼��д���ֶκ�����
![]() ��
��![]() ������ͼ��ķ���һ�����Ѻ���
������ͼ��ķ���һ�����Ѻ���![]() ��ͼ����
��ͼ����![]() �����沿�֣���
�����沿�֣���![]() ����з��ۿɵõ�����
����з��ۿɵõ�����![]() ��ͼ��
��ͼ��
![]() ���û�����ͼ��ͨ��ȷ��
���û�����ͼ��ͨ��ȷ��![]() ��ͼ����ֱ��
��ͼ����ֱ��![]() �Ľ������������⣮
�Ľ������������⣮
��������� ![]() ����������ͼ
����������ͼ![]() ��
��
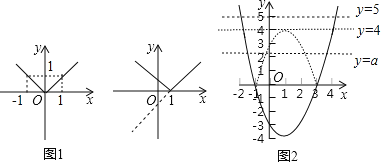
![]() ���̽��
���̽��
������![]() ��ͼ��,����ת��Ϊ�ֶκ���
��ͼ��,����ת��Ϊ�ֶκ���![]()
![]() ��չ���
��չ���
�Ѻ���![]() ��ͼ����
��ͼ����![]() �����沿�֣���
�����沿�֣���![]() ����з��ۿɵõ�������ͼ��
����з��ۿɵõ�������ͼ��
��![]() ���ϼ����沿������˺���
���ϼ����沿������˺���![]() ��ͼ����ͼ
��ͼ����ͼ![]() ��
��
![]() �ٺ���
�ٺ���![]() ��ͼ����
��ͼ����![]() ����
����![]() ������,��Ӧ����
������,��Ӧ����![]() ��
��![]() ��ʵ����
��ʵ����
�ں���![]() ��ͼ����ֱ��
��ͼ����ֱ��![]() ��
��![]() ������,��Ӧ����
������,��Ӧ����![]() ��
��![]() ��ʵ����
��ʵ����
�ۺ���![]() ��ͼ����ֱ��
��ͼ����ֱ��![]() ��
��![]() ������,��Ӧ����
������,��Ӧ����![]() ��
��![]() ��ʵ����
��ʵ����
�ܹ���![]() �ķ���
�ķ���![]() ��
��![]() ��ʵ��ʱ��
��ʵ��ʱ�� ![]() ��ȡֵ��Χ��
��ȡֵ��Χ��![]()
�ʴ�Ϊ�� ![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1������ABC�У���PΪBC���е㣬ֱ��a�ƶ���A��ת����B��P��ֱ��a����࣬BMֱ��a�ڵ�M��CNֱ��a�ڵ�N������PM��PN��
(1) �ӳ�MP��CN�ڵ�E(��ͼ2)����֤����BPM����CPE����֤��PM=PN��
(2) ��ֱ��a�Ƶ�A��ת��ͼ3��λ��ʱ����B��P��ֱ��a��ͬ�࣬�����������䡣��ʱ
PM=PN���������������������֤����������������˵�����ɣ�
(3) ��ֱ��a�Ƶ�A��ת����BC��ƽ�е�λ��ʱ�������������䡣��ֱ���ж��ı���MBCN
����״����ʱPM=PN�������𣿲���˵�����ɡ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�����߳��ֱ���a��b��c����a��b��c����(a��b)2��2ab��c2������ABCΪ________�����Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������P(3,��1)����ƽ��2����λ������ƽ��3����λ��õ���Q�����Q����Ϊ��������
A. ��1����4��B. ��1��2��C. ��5����4��D. ��5��2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ʽx2ym+2��xny�ĺ���Ȼ��һ������ʽ����m��n��ֵ�ǣ�������
A.m=2��n=2
B.m=��1��n=2
C.m=��2��n=2
D.m=2��n=��1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AB=16cm��AD=4cm����P��Q�ֱ��A��Bͬʱ��������P�ڱ�AB����AB������2cm/s���ٶ������˶�����Q�ڱ�BC����BC������1cm/s���ٶ������˶���������һ�㵽���յ�ʱ����һ��Ҳ��ֹ֮ͣ�˶�.���˶�ʱ��Ϊx�룬��PBQ�����Ϊy��cm2��.
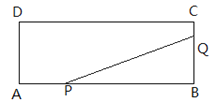
��1����y����x�ĺ�����ϵʽ����д��x��ȡֵ��Χ��
��2������PBQ����������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�ٰ����ҵ��й������ݽ���������9��ѧ���μӱ��������DZ��������ճɼ�������ͬ��ȡǰ5��ͬѧ�μӾ���������һ��ͬѧ֪���Լ��ķ�����Ҫ�ж��Լ��ܷ���������ֻ��Ҫ֪����9��ͬѧ������( )
A. ��λ��B. ����C. ƽ����D. ����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com