
【题目】如图1,在△ABC中,点P为BC边中点,直线a绕顶点A旋转,若B、P在直线a的异侧,BM直线a于点M,CN直线a于点N,连接PM、PN;
(1) 延长MP交CN于点E(如图2)。求证:△BPM≌△CPE;求证:PM=PN;
(2) 若直线a绕点A旋转到图3的位置时,点B、P在直线a的同侧,其它条件不变。此时
PM=PN还成立吗?若成立,请给予证明;若不成立,请说明理由;
(3) 若直线a绕点A旋转到与BC边平行的位置时,其它条件不变。请直接判断四边形MBCN
的形状及此时PM=PN还成立吗?不必说明理由。

【答案】(1)见解析;(2)成立;(3)成立
【解析】
试题分析:(1)①根据平行线的性质证得∠MBP=∠ECP再根据BP=CP,∠BPM=∠CPE即可得到;
②由△BPM≌△CPE,得到PM=PE则PM=![]() ME,而在Rt△MNE中,PN=
ME,而在Rt△MNE中,PN=![]() ME,即可得到PM=PN.
ME,即可得到PM=PN.
(2)证明方法与②相同.
(3)四边形MBCN是矩形,则PM=PN成立.
(1)①如图2:
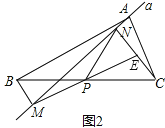
∵BM⊥直线a于点M,CN⊥直线a于点N,
∴∠BMA=∠CNM=90°,
∴BM∥CN,
∴∠MBP=∠ECP,
又∵P为BC边中点,
∴BP=CP,
又∵∠BPM=∠CPE,
∴△BPM≌△CPE,
②∵△BPM≌△CPE,
∴PM=PE
∴PM=![]() ME,
ME,
∴在Rt△MNE中,PN=![]() ME,
ME,
∴PM=PN.
(2)成立,如图3,延长MP与NC的延长线相交于点E,
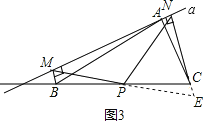
∵BM⊥直线a于点M,CN⊥直线a于点N,
∴∠BMN=∠CNM=90°
∴∠BMN+∠CNM=180°,
∴BM∥CN
∴∠MBP=∠ECP,
又∵P为BC中点,
∴BP=CP,
又∵∠BPM=∠CPE,
∴△BPM≌△CPE,
∴PM=PE,
∴PM=![]() ME,
ME,
则Rt△MNE中,PN=![]() ME,
ME,
∴PM=PN.
(3)如图4:
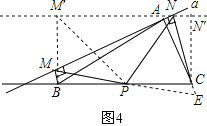
四边形M′BCN′是矩形,
根据矩形的性质和P为BC边中点,得到△M′BP≌△N′CP,
得PM′=PN′成立.即“四边形MBCN是矩形,则PM=PN成立”.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:
【题目】某大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索顶端的距离BC为2米,两拉索底端距离AD为20米,请求出立柱BH的长.(结果精确到0.1米, ![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某饭店在2014年春节年夜饭的预定工作中,第一天预定了a桌,第二天预定的桌数比第一天多了4桌,则这两天该饭店一共预定了 桌年夜饭(用含a的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级七班“数学兴趣小组”对函数的对称变换进行探究,以下是探究发现运用过程,请补充完整.
(1)操作发现
在作函数y=|x|的图象时,采用了分段函数的办法,该函数转化为y=![]() ,请在如图1所示的平面直角坐标系中作出函数的图象;
,请在如图1所示的平面直角坐标系中作出函数的图象;
(2)类比探究
作函数y=|x-1|的图象,可以转化为分段函数y=![]() ,然后分别作出两段函数的图象.聪明的小昕利用坐标平面上的轴对称知识,把函数y=x-1在x轴下面部分,沿x轴进行翻折,与x轴上及上面部分组成了函数y=|x-1|的图象,如图2所示;
,然后分别作出两段函数的图象.聪明的小昕利用坐标平面上的轴对称知识,把函数y=x-1在x轴下面部分,沿x轴进行翻折,与x轴上及上面部分组成了函数y=|x-1|的图象,如图2所示;
(3)拓展提高
如图3是函数y=x2-2x-3的图象,请在原平面直角坐标系作函数y=|x2-2x-3|的图象;
(4)实际运用
①函数y=|x2-2x-3|的图象与x轴有 个交点,对应方程|x2-2x-3|=0有 个实根;
②函数y=|x2-2x-3|的图象与直线y=5有 个交点,对应方程|x2-2x-3|=5有 个实根;
③函数y=|x2-2x-3|的图象与直线y=4有 个交点,对应方程|x2-2x-3|=4有 个实根;
④关于x的方程|x2-2x-3|=a有4个实根时,a的取值范围是 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com