
【题目】在一条东西走向的马路旁,有青少年宫、学校、商场、医院四家公共场所.已知青少年宫在学校东500m处,商场在学校西300m处,医院在学校东600m处.若将马路近似地看作一条直线,以学校为原点,向东方向为正方向,用1个单位长度表示100m.
(1)请画一条数轴并在数轴上表示出四家公共场所的位置;
(2)列式计算青少年宫与商场之间的距离;
(3)若小新家也位于这条马路旁,在青少年宫的西边,且到商场与青少年宫的距离之和等于到医院的距离,试求小新家与学校的距离.
【答案】(1)数轴表示见解析;(2)青少年宫与商场之间的距离800m;(3)小新家与学校的距离为200m或400m.
【解析】试题分析: ![]() 规定向东为正,单位长度是以100米为1个单位,根据青少年宫、学校、商场、医院的位置画出数轴即可,
规定向东为正,单位长度是以100米为1个单位,根据青少年宫、学校、商场、医院的位置画出数轴即可,![]() 根据数轴上两点之间的距离是表示这两点的数的差的绝对值求值即可.
根据数轴上两点之间的距离是表示这两点的数的差的绝对值求值即可.![]() 由题意可得小新家到医院的距离为800m,设小新家在数轴上为
由题意可得小新家到医院的距离为800m,设小新家在数轴上为![]() ,列出方程求出
,列出方程求出![]() ,即可确定小新家与学校的距离.
,即可确定小新家与学校的距离.
试题解析:(1)如图,
![]()
(2)青少年宫与商场之间的距离![]()
(3)①∵小新家在青少年宫的西边,且到商场与青少年宫的距离之和等于到医院的距离,
∴小新家到医院的距离为800m,
设小新家在数轴上为![]() ,则
,则![]() 解得
解得![]()
∴小新家与学校的距离为200m;
②当小新家在商场的西边时,设小新家在数轴上为![]() ,则
,则![]() 解得
解得![]()
∴小新家与学校的距离为400m.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线与x轴交于A(6,0)、B(![]() ,0)两点,与y轴交于点C,过抛物线上点M(1,3)作MN⊥x轴于点N,连接OM.
,0)两点,与y轴交于点C,过抛物线上点M(1,3)作MN⊥x轴于点N,连接OM.
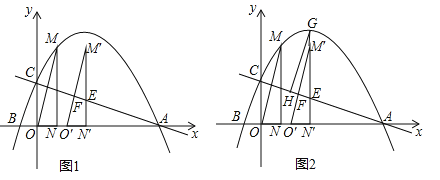
(1)求此抛物线的解析式;
(2)如图1,将△OMN沿x轴向右平移t个单位(0≤t≤5)到△O′M′N′的位置,MN′、M′O′与直线AC分别交于点E、F.
①当点F为M′O′的中点时,求t的值;
②如图2,若直线M′N′与抛物线相交于点G,过点G作GH∥M′O′交AC于点H,试确定线段EH是否存在最大值?若存在,求出它的最大值及此时t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
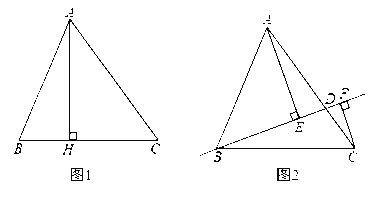
【题目】如图1和2,在△ABC中,AB=13,BC=14,BH=5.
探究:如图1,AH⊥BC于点H,则AH= ,AC= ,△ABC的面积![]() ;
;
拓展:如图2,点D在AC上(可与点A,C重合),分别过点A.C作直线BD的垂线,垂足为E,F,设BD=x,AE=m,CF=n(当点D与点A重合时,我们认为![]() )
)
(1)用含x,m,n的代数式表示![]() 及
及![]() ;
;
(2)求(m+n)与x的函数关系式,并求(m+n)的最大值和最小值;
(3)对给定的一个x值,有时只能确定唯一的点D,直接写出这样的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张正方形纸片剪去四个大小形状一样的小正方形,然后将其中一个小正方形再按同样的方法剪成四个小正方形,再将其中一个小正方形剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环进行下去.
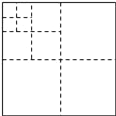
(1)填表:

(2)如果剪了100次,共剪出多少个小正方形?
(3)如果剪n次,共剪出多少个小正方形?
(4)如果要剪出100个正方形,那么需要剪多少次?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() 过B(﹣2,6),C(2,2)两点.
过B(﹣2,6),C(2,2)两点.
(1)试求抛物线的解析式;
(2)记抛物线顶点为D,求△BCD的面积;
(3)若直线![]() 向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,求b的取值范围.
向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,求b的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为a的正方形中挖去一个边长为b的小正方形(a>b)(如图甲),把余下的部分拼成一个矩形(如图乙),根据两个图形中阴影部分的面积相等,可以验证( )

A. (a+b)2=a2+2ab+b2 B. (a﹣b)2=a2-2ab+b2
C. (a+b)(a﹣b)= a2﹣b2 D. (a+2b)(a﹣b)=a2+ab﹣2b2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com