
如下数表是由从1开始的连续自然数组成,观察规律并完成各题的解答.


(1)表中第8行的最后一个数是 ,它是自然数 的平方,第8行共有 个数;
(2)用含n的代数式表示:第n行的第一个数是 ,最后一个数是 ,第n行共有 个数;
(3)求第n行各数之和.
【考点】整式的混合运算;规律型:数字的变化类.
【分析】(1)数为自然数,每行数的个数为1,3,5,…的奇数列,很容易得到所求之数;
(2)知第n行最后一数为n2,则第一个数为n2﹣2n+2,每行数由题意知每行数的个数为1,3,5,…的奇数列,故个数为2n﹣1;
(3)通过以上两步列公式从而解得.
【解答】解:(1)每行数的个数为1,3,5,…的奇数列,由题意最后一个数是该行数的平方即得64,
其他也随之解得:8,15;
(2)由(1)知第n行最后一数为n2,且每行个数为(2n﹣1),则第一个数为n2﹣(2n﹣1)+1=n2﹣2n+2,
每行数由题意知每行数的个数为1,3,5,…的奇数列,
故个数为2n﹣1;
(3)第n行各数之和:
 ×(2n﹣1)=(n2﹣n+1)(2n﹣1).
×(2n﹣1)=(n2﹣n+1)(2n﹣1).
【点评】本题考查了整式的混合运算,(1)看数的规律,自然数的排列,每排个数1,3,5,…从而求得;(2)最后一数是行数的平方,则第一个数即求得;(3)通过以上两步列公式从而解得.本题看规律为关键,横看,纵看.


科目:初中数学 来源: 题型:
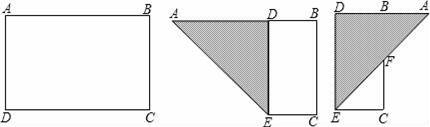
如图,有一块矩形纸片ABCD,AB=8,AD=6,将纸片折叠,使得AD边落在AB边上,折痕为AE,再将△AED沿DE向右翻折,AE与BC的交点为F,则△CEF的面积为( )

A.
 B.
B.
 C.2 D.4
C.2 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
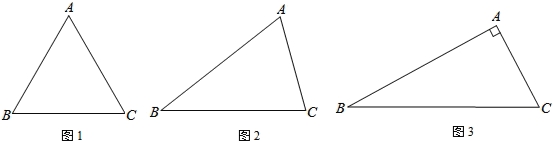
已知:在△ABC中,D为BC边上一点,B,C两点到直线AD的距离相等.
(1)如图1,若△ABC是等腰三角形,AB=AC,则点D的位置在点D为线段BC的中点;
(2)如图2,若△ABC是任意一个锐角三角形,猜想点D的位置是否发生变化,请补全图形并加以证明;
(3)如图3,当△ABC是直角三角形,∠A=90°,并且点D满足(2)的位置条件,用等式表示线段AB,AC,AD之间的数量关系并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com