
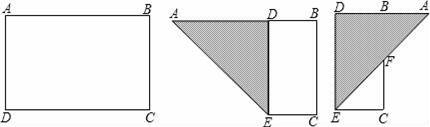
如图,有一块矩形纸片ABCD,AB=8,AD=6,将纸片折叠,使得AD边落在AB边上,折痕为AE,再将△AED沿DE向右翻折,AE与BC的交点为F,则△CEF的面积为( )

A.
 B.
B.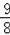
 C.2 D.4
C.2 D.4
C【考点】翻折变换(折叠问题).
【分析】根据折叠的性质,在图②中得到DB=8﹣6=2,∠EAD=45°;在图③中,得到AB=AD﹣DB=6﹣2=4,△ABF为等腰直角三角形,然后根据等腰三角形的性质和矩形的性质得到BF=AB=4,CF=BC﹣BF=6﹣4=2,EC=DB=2,最后根据三角形的面积公式计算即可.
【解答】解:∵AB=8,AD=6,纸片折叠,使得AD边落在AB边上,
∴DB=8﹣6=2,∠EAD=45°,
又∵△AED沿DE向右翻折,AE与BC的交点为F,
∴AB=AD﹣DB=6﹣2=4,△ABF为等腰直角三角形,
∴BF=AB=4,
∴CF=BC﹣BF=6﹣4=2,
而EC=DB=2,
 ×2×2=2.
×2×2=2.
故选:C.

【点评】本题考查了折叠的性质:折叠前后的两个图形全等,即对应线段相等,对应角相等.也考查了等腰三角形的性质和矩形的性质.


科目:初中数学 来源: 题型:
下列事件中,是随机事件的是( )
A.度量四边形的内角和为180°
B.通常加热到100℃,水沸腾
C.袋中有2个黄球,3个绿球,共五个球,随机摸出一个球是红球
D.抛掷一枚硬币两次,第一次正面向上,第二次反面向上
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点.
(1)求该抛物线的解析式;
(2)求该抛物线的对称轴以及顶点坐标;
(3)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
如下数表是由从1开始的连续自然数组成,观察规律并完成各题的解答.


(1)表中第8行的最后一个数是 ,它是自然数 的平方,第8行共有 个数;
(2)用含n的代数式表示:第n行的第一个数是 ,最后一个数是 ,第n行共有 个数;
(3)求第n行各数之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
阅读下面材料:
在数学课上,老师提出如下问题:

小强的作法如下:

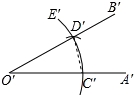
老师说:“小强的作法正确.”
请回答:小强用直尺和圆规作图∠A'′O′B′=∠AOB,根据三角形全等的判定方法中的SSS,
得出△D′O′C′≌△DOC,才能证明∠A′O′B′=∠AOB.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图①,在△ABC中,D、E分别是AB,AC上的点,AB=AC,AD=AE,然后将△ADE绕点A顺时针旋转一定角度,连接BD,CE,得到图②,将BD,CE分别延长至M,N,使DM= BD,EN=
BD,EN= CE,连接AM,AN,MN得到图③,请解答下列问题:
CE,连接AM,AN,MN得到图③,请解答下列问题:
(1)在图②中,BD与CE的数量关系是__________;
(2)在图③中,猜想AM与AN的数量关系,∠MAN与∠BAC的数量关系,并证明你的猜想.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com