
如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点.
(1)求该抛物线的解析式;
(2)求该抛物线的对称轴以及顶点坐标;
(3)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标.

【考点】待定系数法求二次函数解析式;二次函数的性质;二次函数图象上点的坐标特征.
【分析】(1)由于抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,那么可以得到方程x2+bx+c=0的两根为x=﹣1或x=3,然后利用根与系数即可确定b、c的值.
(2)根据S△PAB=8,求得P的纵坐标,把纵坐标代入抛物线的解析式即可求得P点的坐标.
【解答】解:(1)∵抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,
∴方程x2+bx+c=0的两根为x=﹣1或x=3,
∴﹣1+3=﹣b,
﹣1×3=c,
∴b=﹣2,c=﹣3,
∴二次函数解析式是y=x2﹣2x﹣3.
(2)∵y=﹣x2﹣2x﹣3=(x﹣1)2﹣4,
∴抛物线的对称轴x=1,顶点坐标(1,﹣4).
(3)设P的纵坐标为|yP|,
∵S△PAB=8,
∴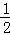 AB•|yP|=8,
AB•|yP|=8,
∵AB=3+1=4,
∴|yP|=4,
∴yP=±4,
把yP=4代入解析式得,4=x2﹣2x﹣3,
解得,x=1±2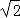 ,
,
把yP=﹣4代入解析式得,﹣4=x2﹣2x﹣3,
解得,x=1,
∴点P在该抛物线上滑动到(1+2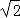 ,4)或(1﹣2
,4)或(1﹣2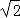 ,4)或(1,﹣4)时,满足S△PAB=8.
,4)或(1,﹣4)时,满足S△PAB=8.
【点评】此题主要考查了利用抛物线与x轴的交点坐标确定函数解析式,二次函数的对称轴点的坐标以及二次函数的性质,二次函数图象上的坐标特征,解题的关键是利用待定系数法得到关于b、c的方程,解方程即可解决问题.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:
在一个不透明的口袋中装有5个完全相同的小球,把它们分别标号为1,2,3,4,5,从中随机摸出一个小球,其标号小于4的概率为( )
A.
 B.
B.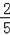
 C.
C.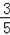
 D.
D.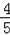

查看答案和解析>>
科目:初中数学 来源: 题型:
在平面直角坐标系中,将抛物线y=x2﹣x﹣6向上(下)或向左(右)平移m个单位,使平移后的抛物线恰好经过原点,则|m|的最小值为( )
A.1 B.2 C.3 D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,有一块矩形纸片ABCD,AB=8,AD=6,将纸片折叠,使得AD边落在AB边上,折痕为AE,再将△AED沿DE向右翻折,AE与BC的交点为F,则△CEF的面积为( )
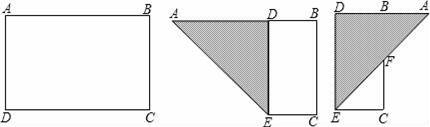

A.
 B.
B.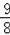
 C.2 D.4
C.2 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
观察 下列关于自然数的等式:
下列关于自然数的等式:
3 -4×1
-4×1 =5 ①
=5 ①
5 -4×2
-4×2 =9 ②
=9 ②
7 -4×3
-4×3 =13 ③
=13 ③
 根据上述规律解决下列问题:
根据上述规律解决下列问题:
(1)完成第四个等式:_________________;
(2)写出你猜想的第n个等式(用含n的式子表示)______________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com