
阅读下面材料:
在数学课上,老师提出如下问题:

小强的作法如下:

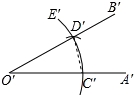
老师说:“小强的作法正确.”
请回答:小强用直尺和圆规作图∠A'′O′B′=∠AOB,根据三角形全等的判定方法中的SSS,
得出△D′O′C′≌△DOC,才能证明∠A′O′B′=∠AOB.
科目:初中数学 来源: 题型:
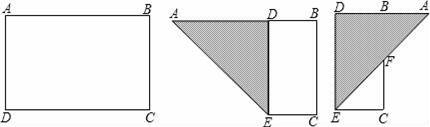
如图,有一块矩形纸片ABCD,AB=8,AD=6,将纸片折叠,使得AD边落在AB边上,折痕为AE,再将△AED沿DE向右翻折,AE与BC的交点为F,则△CEF的面积为( )

A.
 B.
B.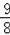
 C.2 D.4
C.2 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
已知:在△ABC中,D为BC边上一点,B,C两点到直线AD的距离相等.
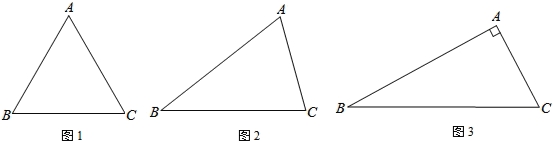
(1)如图1,若△ABC是等腰三角形,AB=AC,则点D的位置在点D为线段BC的中点;
(2)如图2,若△ABC是任意一个锐角三角形,猜想点D的位置是否发生变化,请补全图形并加以证明;
(3)如图3,当△ABC是直角三角形,∠A=90°,并且点D满足(2)的位置条件,用等式表示线段AB,AC,AD之间的数量关系并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
观察 下列关于自然数的等式:
下列关于自然数的等式:
3 -4×1
-4×1 =5 ①
=5 ①
5 -4×2
-4×2 =9 ②
=9 ②
7 -4×3
-4×3 =13 ③
=13 ③
 根据上述规律解决下列问题:
根据上述规律解决下列问题:
(1)完成第四个等式:_________________;
(2)写出你猜想的第n个等式(用含n的式子表示)______________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
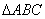 与
与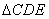 是共顶点的等边三角形. 直线BE与直线AD交于点M,点D、E不在
是共顶点的等边三角形. 直线BE与直线AD交于点M,点D、E不在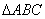 的边上.
的边上.
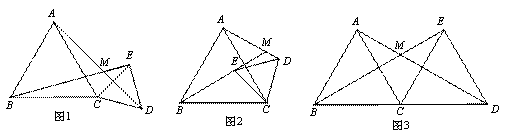
(1)当点E在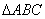 外部时(如图1),写出AD与BE的数量关系.
外部时(如图1),写出AD与BE的数量关系.
(2)若CD<BC,将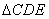 绕着点C逆时针旋转,使得点E由
绕着点C逆时针旋转,使得点E由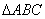 的外部运动到
的外部运动到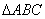 的内部(如图2).在这个运动过程中,
的内部(如图2).在这个运动过程中,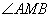 的大小是否发生变化?若不变,在图2的情况下求出
的大小是否发生变化?若不变,在图2的情况下求出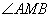 的度数,若变化,说明理由.
的度数,若变化,说明理由.
(3)如图3,当B、C、D三点在同一条直线上,且BC=CD时,写出BM,ME与BC之间的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com