
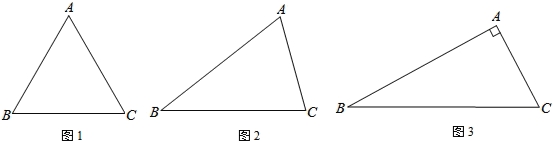
已知:在△ABC中,D为BC边上一点,B,C两点到直线AD的距离相等.
(1)如图1,若△ABC是等腰三角形,AB=AC,则点D的位置在点D为线段BC的中点;
(2)如图2,若△ABC是任意一个锐角三角形,猜想点D的位置是否发生变化,请补全图形并加以证明;
(3)如图3,当△ABC是直角三角形,∠A=90°,并且点D满足(2)的位置条件,用等式表示线段AB,AC,AD之间的数量关系并加以证明.
【考点】全等三角形的判定与性质.
【分析】(1)点D为线段BC的中点,根据线段的中点即可解答;
(2)点D的位置没有发生变化;作BE⊥AD于点E,CF⊥AD于点F,证明△BED≌△CFD,得到BD=DC.即点D是BC边的中点;
(3)AB,AC,AD之间的数量关系为AC2+AB2=4AD2.如图2,延长AD到点H使DH=AD,连接HC.证明△ABD≌△HCD,得到∠1=∠3,AB=CH.再证明∠ACH=90°,得到AC2+CH2=AH2.由DH=AD,得到AC2+AB2=(2AD)2.即可解答.
【解答】解:(1)∵点D为BC边的中点,
∴BD=CD,
故答案为:点D为线段BC的中点;
(2)点D的位置没有发生变化,
证明:如图1,作BE⊥AD于点E,CF⊥AD于点F,

∵BE⊥AD于点E,CF⊥AD于点F,
∴∠3=∠4=90°,
在△BED和△CFD中,

∴△BED≌△CFD.
∴BD=DC.即点D是BC边的中点.
(3)AB,AC,AD之间的数量关系为AC2+AB2=4AD2.
证明:如图2,延长AD到点H使DH=AD,连接HC.

∵点D是BC边的中点,
∴BD=DC.
在△ABD和△HCD中,

∴△ABD≌△HCD.
∴∠1=∠3,AB=CH.
∵∠A=90°,
∴∠1+∠2=90°.
∴∠2+∠3=90°.
∴∠ACH=90°.
∴AC2+CH2=AH2.
又∵DH=AD,
∴AC2+AB2=(2AD)2.
∴AC2+AB2=4AD2.
【点评】本题考查了全等三角形的性质定理与判定定理、勾股定理的应用,解决本题的关键是作出辅助线,构建全等三角形.


 互动英语系列答案
互动英语系列答案科目:初中数学 来源: 题型:
下列事件中,是随机事件的是( )
A.度量四边形的内角和为180°
B.通常加热到100℃,水沸腾
C.袋中有2个黄球,3个绿球,共五个球,随机摸出一个球是红球
D.抛掷一枚硬币两次,第一次正面向上,第二次反面向上
查看答案和解析>>
科目:初中数学 来源: 题型:
如下数表是由从1开始的连续自然数组成,观察规律并完成各题的解答.


(1)表中第8行的最后一个数是 ,它是自然数 的平方,第8行共有 个数;
(2)用含n的代数式表示:第n行的第一个数是 ,最后一个数是 ,第n行共有 个数;
(3)求第n行各数之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
阅读下面材料:
在数学课上,老师提出如下问题:

小强的作法如下:

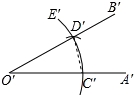
老师说:“小强的作法正确.”
请回答:小强用直尺和圆规作图∠A'′O′B′=∠AOB,根据三角形全等的判定方法中的SSS,
得出△D′O′C′≌△DOC,才能证明∠A′O′B′=∠AOB.
查看答案和解析>>
科目:初中数学 来源: 题型:
中国女药学家屠呦呦获2015年诺贝尔医学奖,她的突出贡献是创制新型抗疟药青蒿素和双氢青蒿素,这是中国医学界迄今为止获得的最高奖项.已知显微镜下的某种疟原虫平均长度为0.0000015米,该长度用科学记数法表示为____米.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图①,在△ABC中,D、E分别是AB,AC上的点,AB=AC,AD=AE,然后将△ADE绕点A顺时针旋转一定角度,连接BD,CE,得到图②,将BD,CE分别延长至M,N,使DM= BD,EN=
BD,EN= CE,连接AM,AN,MN得到图③,请解答下列问题:
CE,连接AM,AN,MN得到图③,请解答下列问题:
(1)在图②中,BD与CE的数量关系是__________;
(2)在图③中,猜想AM与AN的数量关系,∠MAN与∠BAC的数量关系,并证明你的猜想.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com