
【题目】某宾馆有若干间标准房,当标准房的价格为200元时,每天入住的房间数为60间,经市场调查表明,该宾馆每间标准房的价格在170~240元之间(含170元,240元)浮动时,每天入住的房间数![]() (间)与每间标准房的价格
(间)与每间标准房的价格![]() (元)的数据如下表:
(元)的数据如下表:
| … | 190 | 200 | 210 | 220 | … |
| … | 65 | 60 | 55 | 50 | … |

(1)根据所给数据在坐标系中描出相应的点,并画出图象.
(2)求![]() 关于
关于![]() 的函数表达式、并写出自变量
的函数表达式、并写出自变量![]() 的取值范围.
的取值范围.
(3)设客房的日营业额为![]() (元).若不考虑其他因素,问宾馆标准房的价格定为多少元时.客房的日营业额最大?最大为多少元?
(元).若不考虑其他因素,问宾馆标准房的价格定为多少元时.客房的日营业额最大?最大为多少元?
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在等腰![]() 中,
中,![]() .点D,E分别在边AB,BC上,将线段ED绕点E按逆时针方向旋转90得到EF.
.点D,E分别在边AB,BC上,将线段ED绕点E按逆时针方向旋转90得到EF.

(1)如图1,若![]() ,点E与点C重合,AF与DC相交于点O.求证:
,点E与点C重合,AF与DC相交于点O.求证:![]() .
.
(2)已知点G为AF的中点.
①如图2,若![]() ,求DG的长.
,求DG的长.
②若![]() ,是否存在点E,使得
,是否存在点E,使得![]() 是直角三角形?若存在,求CE的长;若不存在,试说明理由.
是直角三角形?若存在,求CE的长;若不存在,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题呈现
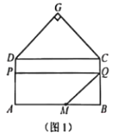
如图,四边形ABCD是矩形,AB=20,BC=10,以CD为一边向矩形外部作等腰直角△GDC,∠G=90°,点M在线段AB上,且AM=a,点P沿折线AD-DG运动,点Q沿折线BC-CG运动(与点G不重合),在运动过程中始终保持线段PQ//AB.设PQ与AB之间的距离为x.
(1)若a=12.①如图1,当点P在线段AD上时,若四边形AMQP的面积为48,则x的值为_________;
②在运动过程中,求四边形AMQP的最大面积;
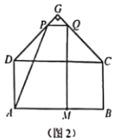
(2)如图2,若点P在线段DG上时,要使四边形AMQP的面积始终不小于50,求a的取值范围.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了解学生对新闻、体育、娱乐、动画四类电视节目的喜爱情况,进行了统计调查![]() 随机调查了某班所有同学最喜欢的节目
随机调查了某班所有同学最喜欢的节目![]() 每名学生必选且只能选择四类节目中的一类
每名学生必选且只能选择四类节目中的一类![]() 并将调查结果绘成如下不完整的统计图
并将调查结果绘成如下不完整的统计图![]() 根据两图提供的信息,回答下列问题:
根据两图提供的信息,回答下列问题:
![]() 最喜欢娱乐类节目的有______人,图中
最喜欢娱乐类节目的有______人,图中![]() ______;
______;
![]() 请补全条形统计图;
请补全条形统计图;
![]() 根据抽样调查结果,若该校有1800名学生,请你估计该校有多少名学生最喜欢娱乐类节目;
根据抽样调查结果,若该校有1800名学生,请你估计该校有多少名学生最喜欢娱乐类节目;
![]() 在全班同学中,有甲、乙、丙、丁等同学最喜欢体育类节目,班主任打算从甲、乙、丙、丁4名同学中选取2人参加学校组织的体育知识竞赛,请用列表法或树状图求同时选中甲、乙两同学的概率.
在全班同学中,有甲、乙、丙、丁等同学最喜欢体育类节目,班主任打算从甲、乙、丙、丁4名同学中选取2人参加学校组织的体育知识竞赛,请用列表法或树状图求同时选中甲、乙两同学的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年5月的第二个星期日即为母亲节,“父母恩深重,恩怜无歇时”,许多市民喜欢在母亲节为母亲送鲜花,感恩母亲,祝福母亲. 节日前夕,某花店采购了一批鲜花礼盒,成本价为30元每件,分析上一年母亲节的鲜花礼盒销售情况,得到了如下数据,同时发现每天的销售量![]() (件)是销售单价
(件)是销售单价![]() (元/件)的一次函数.
(元/件)的一次函数.
销售单价 | … | 30 | 40 | 50 | 60 | … |
每天销售量 | … | 350 | 300 | 250 | 200 | … |
(1)求出![]() 与
与![]() 的函数关系;
的函数关系;
(2)物价局要求,销售该鲜花礼盒获得的利润不得高于100﹪:
①当销售单价![]() 取何值时,该花店销售鲜花礼盒每天获得的利润为5000元?(利润=销售总价-成本价);
取何值时,该花店销售鲜花礼盒每天获得的利润为5000元?(利润=销售总价-成本价);
②试确定销售单价![]() 取何值时,花店销该鲜花礼盒每天获得的利润
取何值时,花店销该鲜花礼盒每天获得的利润![]() (元)最大?并求出花店销该鲜花礼盒每天获得的最大利润.
(元)最大?并求出花店销该鲜花礼盒每天获得的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
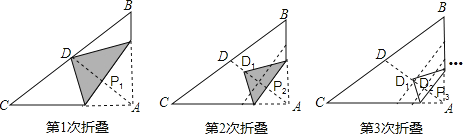
【题目】如图,直角三角形纸片ABC中,AB=3,AC=4.D为斜边BC的中点,第1次将纸片折叠,使点A与点D重合,折痕与AD交于点P1;设P1D的中点为D1,第2次将纸片折叠,使点A与点D1重合,折痕与AD交于点P2;设P2D1的中点为D2,第3次将纸片折叠,使点A与点D2重合,折痕与AD交于点P3;设Pn﹣1Dn﹣2的中点为Dn﹣1,第n次将纸片折叠,使点A与点Dn﹣1重合,折痕与AD交于点Pn(n>2),则AP2019的长为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某新建火车站站前广场需要绿化的面积为46000米2,施工队在绿化了22000米2后,将每天的工作量增加为原来的1.5倍,结果提前4天完成了该项绿化工程.
(1)该项绿化工程原计划每天完成多少米2?
(2)该项绿化工程中有一块长为20米,宽为8米的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为56米2,两块绿地之间及周边留有宽度相等的人行通道(如图所示),问人行通道的宽度是多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,CD是弦,AB⊥CD于E,OF⊥AC于F,BE=OF.
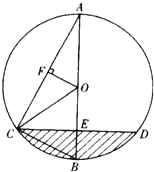
(1)求证:OF∥BC;
(2)求证:△AFO≌△CEB;
(3)若EB=5cm,CD=![]() cm,设OE=x,求x值及阴影部分的面积.
cm,设OE=x,求x值及阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于![]() 的一元二次方程
的一元二次方程![]() ,给出下列说法:①若
,给出下列说法:①若![]() ,则方程必有两个实数根;②若
,则方程必有两个实数根;②若![]() ,则方程必有两个实数根;③若
,则方程必有两个实数根;③若![]() ,则方程有两个不相等的实数根;④若
,则方程有两个不相等的实数根;④若![]() ,则方程一定没有实数根.其中说法正确的序号是( )
,则方程一定没有实数根.其中说法正确的序号是( )
A. ①②③B. ①②④
C. ①③④D. ②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com