
【题目】如图,已知AB为⊙O的直径,CD是弦,AB⊥CD于E,OF⊥AC于F,BE=OF.
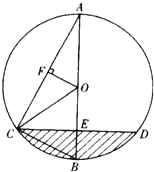
(1)求证:OF∥BC;
(2)求证:△AFO≌△CEB;
(3)若EB=5cm,CD=![]() cm,设OE=x,求x值及阴影部分的面积.
cm,设OE=x,求x值及阴影部分的面积.
【答案】(1)证明见解析(2)证明见解析;(3)![]() ;阴影部分的面积是:
;阴影部分的面积是:![]() cm2.
cm2.
【解析】
(1)根据直径所对的圆周角是直角,以及垂直于同一直线的两直线平行即可证得;
(2)根据垂径定理以及等弧所对的圆周角相等,即可证得:△AFO和△CEB的两个角相等,从而证得两个三角形全等;
(3)根据勾股定理求得x的值,然后根据阴影部分的面积=扇形COD的面积-△COD的面积即可求解.
(1)证明:∵AB为⊙O的直径,
∴AC⊥BC
又∵OF⊥AC
∴OF∥BC
(2)证明:∵AB⊥CD
∴![]()
∴∠CAB=∠BCD
又∵∠AFO=∠CEB=90°,OF=BE,
∴△AFO≌△CEB
(3)连接DO.设OE=x,
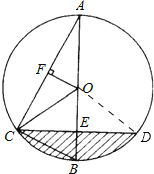
∵AB⊥CD
∴CE=![]() CD=5
CD=5![]() cm.
cm.
在△OCB中,OC=OB=x+5(cm),
根据勾股定理可得:(x+5)2=(5![]() )2+x2
)2+x2
解得:x=5,即OE=5cm,
∴tan∠COE=![]() ,
,
∴∠COE=60°
∴∠COD=120°,
∴扇形COD的面积是:![]() cm2
cm2
△COD的面积是:![]() CDOE=
CDOE=![]() ×10
×10![]() ×5=25
×5=25![]() cm2
cm2
∴阴影部分的面积是:(![]() )cm2.
)cm2.


 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
【题目】艺术节期间,学校向学生征集书画作品,杨老师从全校36个班中随机抽取了4 个班 (用A,B,C,D表示),对征集到的作品的数量进行了统计,制作了两幅不完整的统计图.请 根据相关信息,回答下列问题:
(1)请你将条形统计图补充完整;并估计全校共征集了_____件作品;
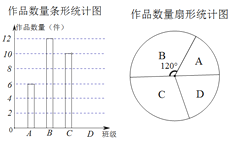
(2)如果全校征集的作品中有4件获得一等奖,其中有3名作者是男生,1名作者是女生,现要在获得一等奖的作者中选取两人参加表彰座谈会,请你用列表或树状图的方法,求选取的两名学生恰好是一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆有若干间标准房,当标准房的价格为200元时,每天入住的房间数为60间,经市场调查表明,该宾馆每间标准房的价格在170~240元之间(含170元,240元)浮动时,每天入住的房间数![]() (间)与每间标准房的价格
(间)与每间标准房的价格![]() (元)的数据如下表:
(元)的数据如下表:
| … | 190 | 200 | 210 | 220 | … |
| … | 65 | 60 | 55 | 50 | … |

(1)根据所给数据在坐标系中描出相应的点,并画出图象.
(2)求![]() 关于
关于![]() 的函数表达式、并写出自变量
的函数表达式、并写出自变量![]() 的取值范围.
的取值范围.
(3)设客房的日营业额为![]() (元).若不考虑其他因素,问宾馆标准房的价格定为多少元时.客房的日营业额最大?最大为多少元?
(元).若不考虑其他因素,问宾馆标准房的价格定为多少元时.客房的日营业额最大?最大为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点P的坐标为(2,0),⊙P与x轴相交于原点O和点A,又B、C两点的坐标分别为(0,b),(﹣1,0).
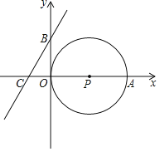
(1)当b=2时,求经过B、C两点的直线解析式;
(2)当B点在y轴上运动时,直线BC与⊙P位置关系如何?并求出相应位置b的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】传统节日“端午节”的早晨,小文妈妈为小文准备了四个粽子作早点:一个枣馅粽,一个肉馅粽,两个花生馅粽,四个粽子除内部馅料不同外,其它一切均相同.
(1)小文吃前两个粽子刚好都是花生馅粽的概率为 ;
(2)若妈妈在早点中给小文再增加一个花生馅的粽子,则小文吃前两个粽子都是花生馅粽的可能性是否会增大?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在综合实践课上,小聪所在小组要测量一条河的宽度,如图,河岸EF∥MN,小聪在河岸MN上点A处用测角仪测得河对岸小树C位于东北方向,然后沿河岸走了30米,到达B处,测得河对岸电线杆D位于北偏东30°方向,此时,其他同学测得CD=10米.请根据这些数据求出河的宽度.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)一个不透明的口袋中装有2个红球(记为红球1、红球2)、1个白球、1个黑球,这些球除颜色外都相同,将球摇匀.
(1)从中任意摸出1个球,恰好摸到红球的概率是 ;
(2)先从中任意摸出1个球,再从余下的3个球中任意摸出1个球,请用列举法(画树状图或列表)求两次都摸到红球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,∠C=30°,以边上AC上一点O为圆心,OA为半径作⊙O,⊙O恰好经过边BC的中点D,并与边AC相交于另一点F.

(1)求证:BD是⊙O的切线.
(2)若AB=![]() ,E是半圆
,E是半圆![]() 上一动点,连接AE,AD,DE.
上一动点,连接AE,AD,DE.
填空:
①当![]() 的长度是____________时,四边形ABDE是菱形;
的长度是____________时,四边形ABDE是菱形;
②当![]() 的长度是____________时,△ADE是直角三角形.
的长度是____________时,△ADE是直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
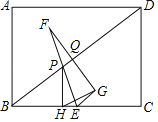
【题目】如图,在矩形ABCD中,AB=6,BC=8,点E是BC的中点,点P为对角线BD上的动点,设BP=t(t>0),作PH⊥BC于点H,连接EP并延长至点F,使得PF=PE,作点F关于BD的对称点G,FG交BD于点Q,连接GH,GE.
(1)求证:EG∥PQ;
(2)当点P运动到对角线BD中点时,求△EFG的周长;
(3)在点P的运动过程中,△GEH是否可以为等腰三角形?若可以,求出t的值;若不可以,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com