
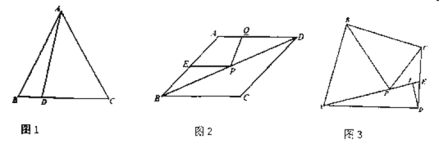
【题目】(1)如图1.等边的边长为2,点![]() 为
为![]() 边上一点,连接
边上一点,连接![]() ,则
,则![]() 长的最小值是________;
长的最小值是________;
(2)如图2,己知菱形![]() 的周长为16,面积为
的周长为16,面积为![]() ,
,![]() 为
为![]() 中点,若
中点,若![]() 为对角线
为对角线![]() 上一动点,
上一动点,![]() 为边
为边![]() 上一动点,计算
上一动点,计算![]() 的最小值;
的最小值;
(3)如图3,己知在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 边上一个动点,连接
边上一个动点,连接![]() ,过点
,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,在
,在![]() 上截取
上截取![]() .试问在四边形
.试问在四边形![]() 内是否存在点
内是否存在点![]() ,使得
,使得![]() 的面积最小?若存在.请你在图中画出点
的面积最小?若存在.请你在图中画出点![]() 的位置,并求出
的位置,并求出![]() 的最小面积;若不存在,请说明理由.
的最小面积;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]() .
.
【解析】
(1)根据垂线段最短即可解决问题.
(2)如图2中,作AH⊥BC于H,在DC上截取DQ′=DQ,连接PQ′,AC,EC.首先证明△ABC是等边三角形,证明△PDQ≌△PDQ′(SAS),可得PQ=PQ′,推出PE+PQ=PE+PQ′,再根据垂线段最短即可解决问题.
(3)存在,如图3中,以AD为斜边在直线AD的下方作等腰直角△ADO,作OM⊥BC于M,AN⊥OM于N,连接AC,PD.证明点P的运动轨迹是![]() ,当点P在线段OM上时,PM的值最小,此时△PBC的面积最小.
,当点P在线段OM上时,PM的值最小,此时△PBC的面积最小.
解:(1)如图1中,根据垂线段最短可知,当AD⊥BC时,线段AD的值最小,
∵△ABC是等边三角形,
∴△ABC的高AD=![]() ,
,
∴AD的最小值为![]() .
.
故答案为:![]() .
.
(2)如图2中,作AH⊥BC于H,在DC上截取DQ′=DQ,连接PQ′,AC,EC.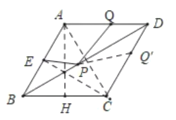
∵四边形ABCD是菱形,周长为16,
∴AB=BC=4,∠QDP=∠Q′DP,
∴S菱形ABCD=BCAH,
∴AH=![]() ,
,
∴sin∠ABH=![]() ,
,
∴∠ABH=60°,
∴△ABC是等边三角形,
∵AE=EB,
∴EC⊥AB,
∵DQ=DQ′,∠PDQ=∠PDQ′,DP=DP,
∴△PDQ≌△PDQ′(SAS),
∴PQ=PQ′,
∴PE+PQ=PE+PQ′,
根据垂线段最短可知,当E,P,Q′共线,且点Q′与C重合时,
PE+PQ′的值最小,最小值=EC=AH=![]() .
.
∴PE+PQ的值最小,最小值为:![]() .
.
(3)存在,理由如下:
如图3中,以AD为斜边在直线AD的下方作等腰直角△ADO,作OM⊥BC于M,AN⊥OM于N,连接AC,PD.
∵BA=BC=![]() ,∠ABC=90°,
,∠ABC=90°,
∴AC=![]() AB=8,∠BAC=45°,
AB=8,∠BAC=45°,
∵∠BAD=75°,
∴∠CAD=30°,
∴AD=ACcos30°=![]() ,
,
∵△ADO是等腰直角三角形,
∴OA=OD=![]() ,
,
∵∠ABM=∠NMB=∠ANM=90°,
∴四边形ABMN是矩形,
∴AB=MN=![]() ,∠BAN=90°,
,∠BAN=90°,
∴∠OAN=75°+45°90°=30°,
∴ON=![]() OA=
OA=![]() ,
,
∴OM=![]() ,
,
∵DF⊥AE,FP=FD,
∴∠FPD=45°,
∴∠APD=135°,
∴点P的运动轨迹是![]() ,
,
当点P在线段OM上时,PM的值最小,此时△PBC的面积最小,
此时PM=OMOP=![]() ,
,
∴△PBC的面积的最小值=![]() BCPM=
BCPM=![]()
![]()
![]() .
.


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
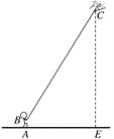
【题目】小明在海湾森林公园放风筝.如图所示,小明在A处,风筝飞到C处,此时线长BC为40米,若小明双手牵住绳子的底端B距离地面1.5米,从B处测得C处的仰角为60°,求此时风筝离地面的高度CE.(计算结果精确到0.1米,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AB=3,BC=5,以点B的圆心,以任意长为半径作弧,分别交BA、BC于点P、Q,再分别以P、Q为圆心,以大于![]() PQ的长为半径作弧,两弧在∠ABC内交于点M,连接BM并延长交AD于点E,则DE的长为_____.
PQ的长为半径作弧,两弧在∠ABC内交于点M,连接BM并延长交AD于点E,则DE的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】绿色出行是对环境影响最小的出行方式,“共享单车”已成为北京的一道靓丽的风景线.某社会实践活动小
组为了了解“共享单车”的使用情况,对本校教师在3月6日至3月10日使用单车的情况进行了问卷调查,
以下是根据调查结果绘制的统计图的一部分:
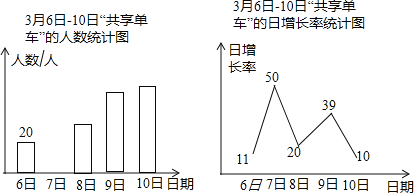
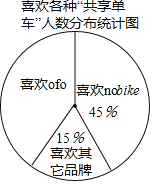
请根据以上信息解答下列问题:
(1)3月7日使用“共享单车”的教师人数为人,并请补全条形统计图;
(2)不同品牌的“共享单车”各具特色,社会实践活动小组针对有过使用“共享单车”经历的教师做了进一步调查,每位教师都按要求选择了一种自己喜欢的“共享单车”,统计结果如图,其中喜欢![]() 的教师有36人,求喜欢
的教师有36人,求喜欢![]() 的教师的人数.
的教师的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场在“五一”促销活动中规定,顾客每消费100元就能获得一次中奖机会.为了活跃气氛.设计了两个抽奖方案:
方案一:转动转盘![]() 一次,转出红色可领取一份奖品;
一次,转出红色可领取一份奖品;
方案二:转动转盘![]() 两次,两次都转出红色可领取一份奖品.(两个转盘都被平均分成3份)
两次,两次都转出红色可领取一份奖品.(两个转盘都被平均分成3份)
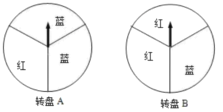
(1)若转动一次![]() 转盘,求领取一份奖品的概率;
转盘,求领取一份奖品的概率;
(2)如果你获得一次抽奖机会,你会选择哪个方案?请采用列表法或树状图说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠A = 30°,AB = m,CD是边AB上的中线,将△ACD沿CD所在直线翻折,得到△ECD,若△ECD与△ABC重合部分的面积等于△ABC面积的![]() ,则△ABC的面积为___________(用m的代数式表示).
,则△ABC的面积为___________(用m的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
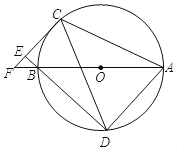
【题目】如图,AB为⊙O的直径,C、D为⊙O上异于A、B的两点,连接CD,过点C作CE⊥DB,交CD的延长线于点E,垂足为点E,直径AB与CE的延长线相交于点F.
(1)连接AC,AD,求证:∠DAC+∠ACF=180°;
(2)若∠ABD=2∠BDC,
①求证:CF是⊙O的切线;
②当BD=6,tanF=![]() 时,求CF的长.
时,求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角三角形![]() 中,
中,![]() ,点
,点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,将
的中点,将![]() 沿
沿![]() 翻折,得到
翻折,得到![]() ,
,![]() 的延长线交
的延长线交![]() 于点
于点![]() .
.
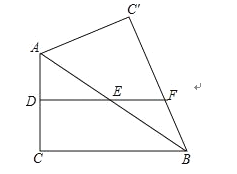
(1)判断![]() 的形状为 ;
的形状为 ;
(2)当![]() 时,求证四边形
时,求证四边形![]() 为正方形;
为正方形;
(3)若![]() ,连接
,连接![]() ,当
,当![]() 时,直接写出
时,直接写出![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形![]() 中,对角线
中,对角线![]() ,
,![]() ,动点
,动点![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 同时出发,运动速度都是
同时出发,运动速度都是![]() ,点
,点![]() 由
由![]() 向
向![]() 运动;点
运动;点![]() 由
由![]() 向
向![]() 运动,当
运动,当![]() 到达
到达![]() 时,
时,![]() 、
、![]() 两点运动停止,设时间为
两点运动停止,设时间为![]() 秒(
秒(![]() ).连接
).连接![]() ,
,![]() ,
,![]() .
.
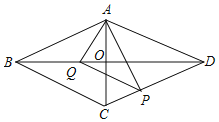
(1)当![]() 为何值时,
为何值时,![]() ;
;
(2)设![]() 的面积为
的面积为![]() ,请写出
,请写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)当![]() 为何值时,
为何值时,![]() 的面积是四边形
的面积是四边形![]() 面积的
面积的![]() ?
?
(4)是否存在![]() 值,使得线段
值,使得线段![]() 经过
经过![]() 的中点
的中点![]() ?若存在,求出
?若存在,求出![]() 值;若不存在,请说明理由.
值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com