
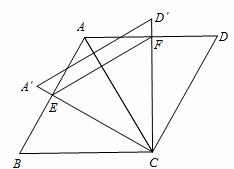
如图,菱形ABCD中,边长为2,∠B=60°,将△ACD绕点C旋转,当AC(即A′C)与AB交于一点E,CD(即CD′)同时与AD交于一点F时,点E,F和点A构成△AEF。试探究△AEF的周长是否存在最小值,如果不存在,请说明理由;如果存在,请计算出△AEF周长的最小值。


解:△AEF的周长存在最小值 。理由
。理由 如下:
如下:
根据菱形和 旋转的性质,以及∠B=60°,可得△ABC,△ACD和△A′CD′是等边三角形,
旋转的性质,以及∠B=60°,可得△ABC,△ACD和△A′CD′是等边三角形,
∴∠BCA=∠BCE+∠ACE=60°,∠ECF=∠ACF+∠ACE=60° 。∴∠BCE=∠ACF。
。∴∠BCE=∠ACF。
在△BCE与△ACF中,BC=AC,∠EBC= ∠
∠ FAC
FAC =60°,∠BCE=∠ACF,
=60°,∠BCE=∠ACF,
∴△BCE≌△ACF(AS A)。∴BE=AF,CE=CF,AE+AF=AE+BE=AB。
A)。∴BE=AF,CE=CF,AE+AF=AE+BE=AB。
∵∠ECF=60°,故△ECF是等边三角形,EF=CF。
∵CF的最小值为点C到AD的距离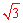 (如图
(如图 ),∴EF的最小
),∴EF的最小 值是
值是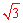 。
。
∵△AEF的周长=AE+AF+EF=AB+EF,∴△AEF的周长的最小值为2+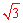 。
。
【考点】旋转的性质,菱形的性质,全等三角形的判定和性质,等边三角形的判定和性质,点到直线 距离的性质。
距离的性质。



科目:初中数学 来源: 题型:
如图,抛物线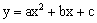 关于直线
关于直线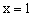 对称,与坐标轴交于A、B、C三点,且AB=4,点D
对称,与坐标轴交于A、B、C三点,且AB=4,点D 在抛物线上,直线
在抛物线上,直线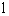 是一次函数
是一次函数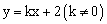 的图象,点O是坐标原点。
的图象,点O是坐标原点。
(1)求抛物线的解析式;
(2)把抛物线向左平移1个单位,再向上平移4个单位,所得抛物线与直线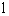 交于M、N两点,问在y轴负半轴上是否存在一定点P,使得不论k取何值,直线PM与PN总是关于y轴
交于M、N两点,问在y轴负半轴上是否存在一定点P,使得不论k取何值,直线PM与PN总是关于y轴 对称?若存在,求出P点坐标;若不存在,请说明理
对称?若存在,求出P点坐标;若不存在,请说明理 由.
由.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面坐标系中,直线y=﹣x+2与x轴,y轴分别交于点A,点B,动点P(a,b)在第一象限内,由点P向x轴,y轴所作的垂线PM,PN(垂足为M,N) 分别与直线AB相交于点E,点F,
分别与直线AB相交于点E,点F, 当点P(a,b)运动时,矩形PMON的面积为定值2.当点E,F都在线段AB上时,由三条线段AE,EF,BF组成一个三角形,记此三角形的外接圆面积为S1,△OEF的面积为S2。试探究:
当点P(a,b)运动时,矩形PMON的面积为定值2.当点E,F都在线段AB上时,由三条线段AE,EF,BF组成一个三角形,记此三角形的外接圆面积为S1,△OEF的面积为S2。试探究: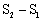 是否存在最大值?若存在,请求出该最大值;若不存在,请说明理由。
是否存在最大值?若存在,请求出该最大值;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,A、B两点的坐标分别是(8,0)、(0,6),点P由点B出发沿BA方向向点A作匀速直线运动,速度为每秒3个单位长度,点Q由A出发沿AO(O为坐标原点)方向向点O作匀速直线 运动,速度为每秒2个单位长度,连接PQ,若设运动时间为t(0<t<
运动,速度为每秒2个单位长度,连接PQ,若设运动时间为t(0<t<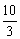
 )秒
)秒 .解答如下问题:
.解答如下问题:


(1)当t为何值 时,PQ∥BO?
时,PQ∥BO?
(2)设△AQP的面积为S,
①求S与t之间的函数关系式,并求出S的最大值;
② 若我们规定:点P、Q的坐标分别为(x1,y1),(x2,y2),则新坐标(x2﹣x1,y2﹣y1)称为“向量PQ”的坐标.当S取最大值时,求“向量PQ”的坐标.
若我们规定:点P、Q的坐标分别为(x1,y1),(x2,y2),则新坐标(x2﹣x1,y2﹣y1)称为“向量PQ”的坐标.当S取最大值时,求“向量PQ”的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,正方形AOCB在平面直角坐标系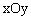 中,点O为原点,点B在反比例函数
中,点O为原点,点B在反比例函数 (
(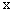 >
>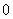 )图象上,
)图象上, OB=
OB= (OC>OA).
(OC>OA).
( 1)
1) 求点B的坐标;
求点B的坐标;
(2)若动点E从A开始沿AB向B以每秒2个单位的速度运动,同时动点F 从B开始沿BC向C以每秒1个单位的速度运动,当其中一个动点到达端点时,另一个动点随之停止运动.当运动 时间为
时间为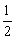 秒时,在x轴上是否
秒时,在x轴上是否 存在点P,使△PEF的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.
存在点P,使△PEF的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在 边长为4的正方形ABCD中,动点E以每秒1个单位长度的速度从点A开始沿边AB向点B运动,动点F以每秒2个单位长度的速度从点B开始沿折线BC﹣CD向点D运动,动点E比动点F先出发1秒,其中一个动点到达终点时,另一个动点也随之停止运动,设点F的运动时间为t秒.
边长为4的正方形ABCD中,动点E以每秒1个单位长度的速度从点A开始沿边AB向点B运动,动点F以每秒2个单位长度的速度从点B开始沿折线BC﹣CD向点D运动,动点E比动点F先出发1秒,其中一个动点到达终点时,另一个动点也随之停止运动,设点F的运动时间为t秒.
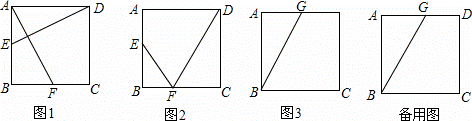

(1)点F在边BC上.
①如图1,连接DE,AF,若DE⊥AF,求t的值;
②如图2,连结EF,DF,当t为何值时,△EBF与△DCF相似?
(2)如图3,若点G是边AD的中点,BG,EF相交于点O,试探究:是否存在在某一时刻t,使得
 ?若存在,求出t
?若存在,求出t 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平面直角坐标系xOy中,A
如图,在平面直角坐标系xOy中,A (2,0),B(4,0),动点C在直线
(2,0),B(4,0),动点C在直线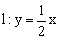 上,若以A、B、C三点为顶点的三角形是等腰三角形,则点C的个数是【 】
上,若以A、B、C三点为顶点的三角形是等腰三角形,则点C的个数是【 】
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在直角坐标系中,点A的坐标为(8,0),点 B(t,b)在直线y=b上运动,点D、E、F分别为OB、OA、AB的中点,其中b是大于零的常数。设直线y=b与y轴交于点C,问:四边形DEFB能不能是矩形?若能,求出t的值;若不能,说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,小球P从(3,0)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当小球P第一次碰到点(3,0)时,小球P所经过的路程为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com