如图，小球P从（3，0）出发，沿所示方向运动，每当碰到矩形的边时反弹，反弹时反射角等于入射角，当小球P第一次碰到点（3，0）时，小球P所经过的路程为 ．
科目：初中数学 来源： 题型：
如图，菱形ABCD中，边长为2，∠B=60°，将△ACD绕点C旋转，当AC（即A′C）与AB交于一点E，CD（即CD′）同时与AD交于一点F时，点E，F和点A构成△AEF。试探究△AEF的周长是否存在最小值，如果不存在，请说明理由；如果存在，请计算出△AEF周长的最小值。
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，直线l1与x轴、y轴分别交于A、B两点，直线l2与直线l1关于x轴对称，已知直线l1的解析式为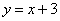
．
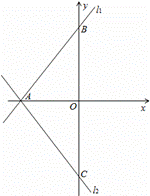
（1）
求直线l2的解析式；
（2）过A点在△ABC的外部作一条直线l3，过点B作BE⊥l3于E，过点C作CF⊥l3于F，请画出图形并求证：BE+CF=EF；
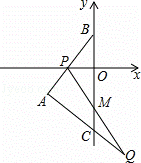
（3）△ABC沿y轴向下平移，AB边交x轴于点P，过P点的直线与AC边的延长线相交于点Q，与y轴相交于点M，且BP=CQ，在△ABC平移的过程中，①OM为定值；②MC为定值．在这两个结论中，有且只有一个是正确的，请找出正确的结论，并求出其值．
查看答案和解析>>
科目：初中数学 来源： 题型：
正方形ABCD中，点E、F分别是边AD、AB的中点，连接EF.
（1）如图1，若点G是边BC的中点，连接FG，则EF与FG关系为： ；
（2）如图2，若点P为BC延长线上一动点，连接FP，将线段FP以点F为旋转中心,逆时针旋转900，得到线段FQ，连接EQ，请猜想EF、EQ、BP三者之间的数量关系，并证明你的结论；
（3）若点P为CB延长线上一动点，按照（2）中的作法，在图3中补全
图形，并直接写出EF、EQ、BP三者之间的数量关系： .
查看答案和解析>>
科目：初中数学 来源： 题型：
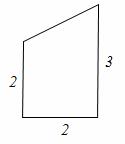
在一张直角三角形纸片的两直角边上各取一点，分别沿斜边中点与这两点的连线剪去两个三角形，剩下的部分是如图所示的直角
梯形，其中三边长分别为2、2、3，则原直角三角形纸片
的斜边长是 。
查看答案和解析>>
科目：初中数学 来源： 题型：
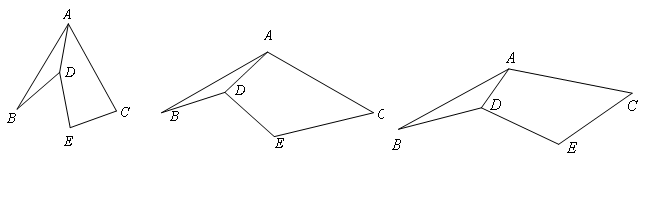
已知AB＝AC，DB＝DE，∠BAC＝∠BDE＝α．
(1)．如图1，α＝60°，探究线段CE与AD
的数量关系，并加以证明；
(2)．如图2，α＝120°，探究线段CE与AD的数量关系，并说明理由；
(3)．如图3，结合上面的活动经验探究线段CE与AD的数量关系为__________ 
．（直接写
出答案）．
查看答案和解析>>
科目：初中数学 来源： 题型：
对于
实数x，我们规定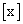
表示不大于x的
最大整数，如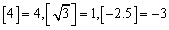
，现对82进行如下操作：
，这样对82只需进行
3次操作后变为1，类似地，①对121只需进行 次操作后变为1；②只需进行3次操作后变为1的所有正整数中，最大的是
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
。
始，分别在各射线上标记点A1、A2、A
3、…，按此规律，点A2014在射 上。
