
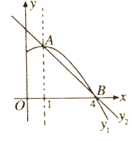
【题目】如图是抛物线![]() 图象的一部分,抛物线的顶点是
图象的一部分,抛物线的顶点是![]() ,对称轴是直线
,对称轴是直线![]() ,且抛物线与
,且抛物线与![]() 轴的一个交点为
轴的一个交点为![]() ;直线
;直线![]() 的解析式为
的解析式为![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③方程
;③方程![]() 有两个不相等的实数根;④抛物线与
有两个不相等的实数根;④抛物线与![]() 轴的另一个交点是
轴的另一个交点是![]() ;⑤当
;⑤当![]() 时,则
时,则![]() .其中正确的是( )
.其中正确的是( )
A.①②B.①③⑤C.①④D.①④⑤
【答案】B
【解析】
根据二次函数的性质分别进行判断,由对称轴可以判断①;由开口方向、对称轴、与y轴的交点坐标,可判断②;由图像可知与直线有两个交点,可判断③;由对称轴可以得到另一个交点,可判断④,结合图像,即可判断⑤,即可得到答案.
解:①因为抛物线对称轴是直线x=1,则![]() ,2a+b=0,故①正确,符合题意;
,2a+b=0,故①正确,符合题意;
②∵抛物线开口向下,故a<0,
∵对称轴在y轴右侧,故b>0,
∵抛物线与y轴交于正半轴,故c>0,
∴abc<0,
故②错误,不符合题意;
③从图象看,两个函数图象有两个交点,故方程ax2+bx+c=mx+n有两个不相等的实数根,正确,符合题意;
④因为抛物线对称轴是:直线x=1,B(4,0),
∴抛物线与x轴的另一个交点是(-2,0),
故④错误,不符合题意;
⑤由图象得:当1<x<4时,有y2<y1,故⑤正确,符合题意;
故正确的有:①③⑤;
故选:B.


科目:初中数学 来源: 题型:
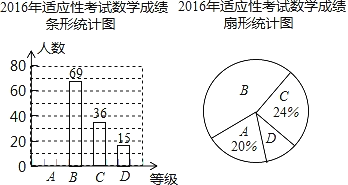
【题目】某校为了解九年级学生2020年适应性考试数学成绩,现从九年级学生中随机抽取部分学生的适应性考试数学成绩,按A,B,C,D四个等级进行统计,并将统计结果绘制成如图所示不完整的统计图.请根据统计图中的信息解答下列问题:
(1)此次抽查的学生人数为 ;
(2)把条形统计图和扇形统计图补充完整;
(3)若该校九年级有学生1200人.请估计在这次适应性考试中达到B等级以上(含B等级)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某月食品加工厂以2万元引进一条新的生产加工线.已知加工这种食品的成本价每袋20元,物价部门规定:该食品的市场销售价不得高于每袋35元,若该食品的月销售量y(千袋)与销售单价x(元)之间的函数关系为:y=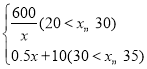 (月获利=月销售收入﹣生产成本﹣投资成本).
(月获利=月销售收入﹣生产成本﹣投资成本).
(1)当销售单价定位25元时,该食品加工厂的月销量为多少千袋;
(2)求该加工厂的月获利M(千元)与销售单价x(元)之间的函数关系式;
(3)求销售单价范围在30<x≤35时,该加工厂是盈利还是亏损?若盈利,求出最大利润;若亏损,最小亏损是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】折纸是一种许多人熟悉的活动.近些年,经过许多人的努力,已经找到了多种将正方形折纸的一边三等分的精确折法,下面探讨其中的一种折法:
(综合与实践)
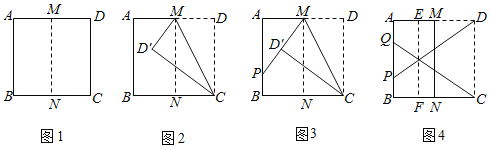
操作一:如图1,将正方形纸片ABCD对折,使点A与点D重合,点B与点C重合,再将正方形纸片ABCD展开,得到折痕MN;
操作二:如图2,将正方形纸片ABCD的右上角沿MC折叠,得到点D的对应的点为D′;
操作三:如图3,将正方形纸片ABCD的左上角沿MD′折叠再展开,折痕MD′与边AB交于点P;
(问题解决)
请在图3中解决下列问题:
(1)求证:BP=D′P;
(2)AP:BP= ;
(拓展探究)
(3)在图3的基础上,将正方形纸片ABCD的左下角沿CD′折叠再展开,折痕CD′与边AB交于点Q.再将正方形纸片ABCD过点D′折叠,使点A落在AD边上,点B落在BC边上,然后再将正方形纸片ABCD展开,折痕EF与边AD交于点E,与边BC交于点F,如图4.试探究:点Q与点E分别是边AB,AD的几等分点?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国是世界上13个贫水国家之一.某校有800名在校学生,学校为鼓励学生节约用水,展开“珍惜水资源,节约每一滴水”系列教育活动.为响应学校号召,数学小组做了如下调查:
小亮为了解一个拧不紧的水龙头的滴水情况,记录了滴水时间和烧杯中的水面高度,如图1.小明设计了调查问卷,在学校随机抽取一部分学生进行了问卷调查,并制作出统计图.如图2和图3.
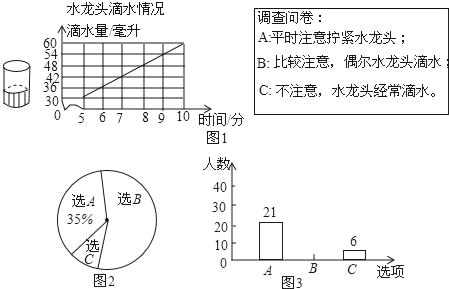
经结合图2和图3回答下列问题:
(1)参加问卷调查的学生人数为 人,其中选C的人数占调查人数的百分比为 .
(2)在这所学校中选“比较注意,偶尔水龙头滴水”的大概有 人.若在该校随机抽取一名学生,这名学生选B的概率为 .
请结合图1解答下列问题:
(3)在“水龙头滴水情况”图中,水龙头滴水量(毫升)与时间(分)可以用我们学过的哪种函数表示?请求出函数关系式.
(4)为了维持生命,每人每天需要约2400毫升水,该校选C的学生因没有拧紧水龙头,2小时浪费的水可维持多少人一天的生命需要?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店购进一批优质晚熟芒果,进价为10元/千克,售价不低于15元/千克,且不超过40元/千克,根据销售情况发现该芒果在一天内的销售量y(千克)与该天的售价x(元/千克)之间满足如表所示的一次函数关系:

(1)写出销售量y与售价x之间的函数关系式;
(2)设某天销售这种芒果获利W元,写出W与售价x之间的函数关系式,并求出当售价为多少元时,当天的获利最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
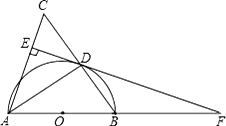
【题目】如图,在△ABC中,AB=AC,以AB为直径作半圆⊙O,交BC于点D,连接AD、过点D作DE⊥AC,垂足为点E,交AB的延长线于点F.
(1)求证:EF是⊙O的切线;
(2)求证:△FDB∽△FAD;
(3)如果⊙O的半径为5,sin∠ADE=![]() ,求BF的长.
,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
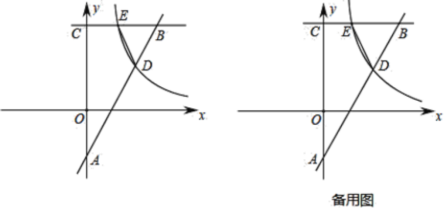
【题目】Rt△OBC在直角坐标系内的位置如图所示,点C在y轴上,∠OCB=90°,反比例函数y=![]() (k>0)在第一象限内的图象与OB边交于点D(m,3),与BC边交于点E(n,6).
(k>0)在第一象限内的图象与OB边交于点D(m,3),与BC边交于点E(n,6).
(1)求m与n的数量关系;
(2)连接CD,若△BCD的面积为12,求反比例函数的解析式和直线OB的解析式;
(3)设点P是线段OB边上的点,在(2)的条件下,是否存在点P,使得以B、C、P为项点的三角形与△BDE相似?若存在,求出此时点P户的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古希腊著名的毕达哥拉斯学派把1、3、6、10 …,这样的数称为“三角形数”,而把1、4、9、16…,这样的数称为“正方形数”.
(1)第5个三角形数是 ,第n个“三角形数”是 ,第5个“正方形数”是 ,第n个正方形数是 ;
(2)经探究我们发现:任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.
例如:①4=1+3,②9=3+6,③16=6+10,④ ,⑤ ,….
请写出上面第4个和第5个等式;
(3)在(2)中,请探究第n个等式,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com