
【题目】期末考试后,某市第一中学为了解本校九年级学生期末考试数学学科成绩情况,决定对该年级学生数学学科期末考试成绩进行抽样分析,已知九年级共有12个班,每班48名学生,请按要求回答下列问题:
(收集数据)
(1)若要从全年级学生中抽取一个48人的样本,你认为以下抽样方法中比较合理的有 ;(只要填写序号即可)
①随机抽取一个班级的48名学生;②在全年级学生中随机抽取48名学生;③在全年级12个班中分别各抽取4名学生;④从全年级学生中随机抽取48名男生;
(整理数据)
(2)将抽取的48名学生的成绩进行分组,绘制频数分布表和成绩分布扇形统计图(不完整)如下.请根据图表中数据填空:
①C类和D类部分的圆心角度数分别为 、
②估计全年级A、B类学生大约一共有 名;

成绩(分) | 频数 | 频率 |
A类(80~100) | 0.5 | |
B类(60~79) | 0.25 | |
C类(40~59) | 8 | |
D类(0~39) | 4 |
(3)学校为了解其他学校教学情况,将同层次的第一、第二两所中学的抽样数据进行对比,得下表:
学校 | 平均分(分) | 极差(分) | 方差 | A、B类的频率和 |
第一中学 | 71 | 52 | 432 | 0.75 |
第二中学 | 71 | 80 | 497 | 0.82 |
你认为哪所学校的教学效果较好?结合数据,请给出一个解释来支持你的观点.
【答案】(1)②③;(2)①60°;30°;②432;(3)从方差角度或A、B类优秀生的角度说明.
【解析】
(1)根据抽取得学生必须有代表性,能反映全年级学生的情况,可以采取随机抽样或随机分层抽样,据此即可得出正确答案;
(2)①利用抽取的学生数及C、D类的频数即可得出C、D类部分的频率,乘以360度可得答案;②用全年级总人数乘以样本中A、B类频率和即可得;
(3)此题答案不唯一,理由正确即可.
(1)根据题意得:抽取得学生②和③更具有代表性,更能反映全年级学生的情况;
故答案为:②③;
(2)表格补充如下
成绩(分) | 频数 | 频率 |
A类(80~100) | 24 | 0.5 |
B类(60~79) | 12 | 0.25 |
C类(40~59) | 8 |
|
D类(0~39) | 4 |
|
①C类部分的频率为:![]() ,故圆心角度数为:
,故圆心角度数为:![]()
D类部分的频率为:![]() ,故圆心角度数为:
,故圆心角度数为:![]()
故答案为:60°、30°.
②A、B类所占的比为:0.5+0.25=0.75
故A、B类所占的人数为:12×48×0.75=432(人)
故答案为:432(人)
(3)本小题答案不唯一,可以从如下两个方面说明:
答案一:东海中学成绩较好,极差、方差小于南山中学,说明东海中学学生两极分化较小,学生之间的差距较南山中学小.
答案二:南山中学成绩较好,A、B类的频率和大于东海中学,说明南山中学学生及格率较东海中学学生好.


科目:初中数学 来源: 题型:
【题目】某商店出售一款商品,经市场调查反映,该商品的日销售量y(件)与销售单价x(元)之间满足一次函数关系,关于该商品的销售单价,日销售量,日销售利润的部分对应数据如表:[注:日销售利润=日销售量×(销售单价﹣成本单价)
销售单价x(元) | 75 | 78 | 82 |
日销售量y(件) | 150 | 120 | 80 |
日销售利润w(元) | 5250 | a | 3360 |
(1)根据以上信息,填空:该产品的成本单价是 元,表中a的值是 ,y关于x的函数关系式是 ;
(2)求该商品日销售利润的最大值.
(3)由于某种原因,该商品进价降低了m元/件(m>0),该商店在今后的销售中,商店规定该商品的销售单价不低于68元,日销售量与销售单价仍然满足(1)中的函数关系,若日销售最大利润是6600元,直接写出m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在ABCD中,DE平分∠ADB,交AB于E,BF平分∠CBD,交CD于F.
(1)求证:△ADE≌△CBF;
(2)当AD与BD满足什么关系时,四边形DEBF是矩形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
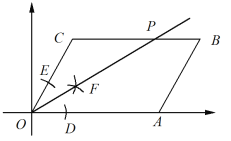
【题目】如图,在平面直角坐标系中,平行四边形OABC的顶点A在x轴上,OC=4,∠AOC=60°,且以点O为圆心,任意长为半径画弧,分别交OA、OC于点D、E;再分别以点D、点E为圆心,大于![]() DE的长度为半径画弧,两弧相交于点F,过点O作射线OF,交BC于点P.则点P的坐标为( )
DE的长度为半径画弧,两弧相交于点F,过点O作射线OF,交BC于点P.则点P的坐标为( )
A.(4,2![]() )B.(6,2
)B.(6,2![]() )C.(2
)C.(2![]() ,4)D.(2
,4)D.(2![]() ,6)
,6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC和△ADE是两个不全等的等腰直角三角形,其中AB=AC,AD=AE,
∠BAC=90°,∠DAE=90°.
(1)观察猜想
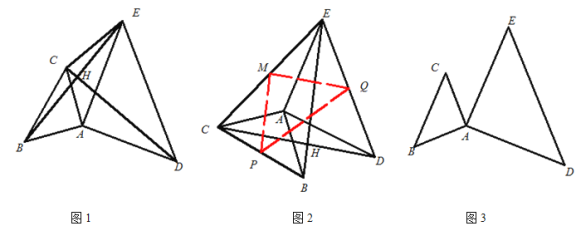
如图1,连接BE、CD交于点H,再连接CE,那么BE和CD的数量关系和位置关系分别是
(2)探究证明
将图1中的△ABC绕点A逆时针旋转到图2的位置时,分别取BC、CE、DE的中点P、M、Q,连接MP、PQ、MQ,请判断MP和MQ的数量关系和位置关系,并说明理由;
(3)拓展延伸
已知AB=![]() ,AD=4,在(2)的条件下,将△ABC绕点A旅转的过程中,若∠CAE=45°,请直接写出此时线段PQ的长.
,AD=4,在(2)的条件下,将△ABC绕点A旅转的过程中,若∠CAE=45°,请直接写出此时线段PQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“新冠肺炎防控”知识宣传活动中,某社区对居民掌握新冠肺炎防控知识的情况进行调查.其中![]() 、
、![]() 两区分别有500名居民,社区从中各随机抽取50名居民进行相关知识测试,并将成绩进行整理得到部分信息:
两区分别有500名居民,社区从中各随机抽取50名居民进行相关知识测试,并将成绩进行整理得到部分信息:
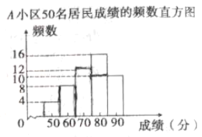
(信息一)![]() 小区50名居民成绩的频数直方图如图(每一组含前一个边界值,不含后一个边界值);
小区50名居民成绩的频数直方图如图(每一组含前一个边界值,不含后一个边界值);
(信息二)图中,![]() 小区从左往右第四组的成绩如下
小区从左往右第四组的成绩如下
75 | 75 | 79 | 79 | 79 | 79 | 80 | 80 |
81 | 82 | 82 | 83 | 83 | 84 | 84 | 84 |
(信息三)![]() 、
、![]() 两小区各50名居民成绩的平均数、中位数、众数、优秀率(80分及以上为优秀)、方差等数据如下(部分空缺):
两小区各50名居民成绩的平均数、中位数、众数、优秀率(80分及以上为优秀)、方差等数据如下(部分空缺):
小区 | 平均数 | 中位数 | 众数 | 优秀率 | 方差 |
| 75.1 | 79 |
| 277 | |
| 75.1 | 77 | 76 |
| 211 |
根据以上信息,回答下列问题:
(1)求![]() 小区50名居民成绩的中位数;
小区50名居民成绩的中位数;
(2)请估计![]() 小区500名居民中能超过平均数的有多少人?
小区500名居民中能超过平均数的有多少人?
(3)请尽量从多个角度比较、分析![]() ,
,![]() 两小区居民掌握新冠防控知识的情况.
两小区居民掌握新冠防控知识的情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县为落实“精准扶贫惠民政策”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合作施工15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙两队合作完成.则甲、乙两队合作完成该工程需要多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校九年级男生的体能情况,体育老师从中随机抽取部分男生进行引体向上测试,并对成绩进行了统计,绘制成尚不完整的扇形图和条形图,根据图形信息回答下列问题:
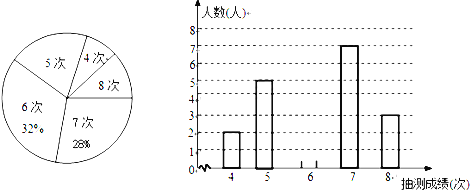
(1)本次抽测的男生有________人,抽测成绩的众数是_________;
(2)请将条形图补充完整;
(3)若规定引体向上6次以上(含6次)为体能达标,则该校125名九年级男生中估计有多少人体能达标?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com