
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| 时间段 | 7~8点 | 8~9点 | 9~10点 | 10~11点 | 11~12点 |
| 数量/辆 | 68 | 56 | 50 | 68 | 54 |
| A. | 56,68 | B. | 68,56 | C. | 68,55 | D. | 68,50 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
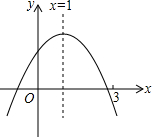 二次函数y=ax2+bx+c(a≠0)图象如图所示.下列结论中,错误的是( )
二次函数y=ax2+bx+c(a≠0)图象如图所示.下列结论中,错误的是( )| A. | abc<0 | |
| B. | 当m≠1时,a+b>am2+bm | |
| C. | 2a+b=0 | |
| D. | 若ax12+bx1=ax22+bx2且x1≠x2,x1+x2=3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在一次抽奖活动中,主办方将奖品随机的放在如图所示的黑白相间的正方形小窗后,如果这次抽奖共分三等,其中一等奖1个,二等奖2相,三等奖3个,那么第一个抽奖人推开一扇黑色小窗能够得到一等奖奖品的概率为$\frac{1}{21}$.
在一次抽奖活动中,主办方将奖品随机的放在如图所示的黑白相间的正方形小窗后,如果这次抽奖共分三等,其中一等奖1个,二等奖2相,三等奖3个,那么第一个抽奖人推开一扇黑色小窗能够得到一等奖奖品的概率为$\frac{1}{21}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com