
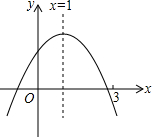 二次函数y=ax2+bx+c(a≠0)图象如图所示.下列结论中,错误的是( )
二次函数y=ax2+bx+c(a≠0)图象如图所示.下列结论中,错误的是( )| A. | abc<0 | |
| B. | 当m≠1时,a+b>am2+bm | |
| C. | 2a+b=0 | |
| D. | 若ax12+bx1=ax22+bx2且x1≠x2,x1+x2=3 |
分析 根据抛物线的对称性得到抛物线的对称轴为直线x=1,根据抛物线对称轴方程得到-$\frac{b}{2a}$=1,则可对C进行判断;由抛物线开口方向得到a<0,由b=-2a得到b>0,由抛物线与y轴的交点在x轴上方得到c>0,则可对A进行判断;利用x=1时,函数有最大值对B进行判断;根据二次函数图象的对称性得到抛物线与x轴的交点(x1,0),(x2,0),于是可对D进行判断.
解答 解:∵抛物线开口方向,
∴a<0,
∵抛物线的对称性得到抛物线的对称轴为直线x=1,
∴2a+b=0,故C正确;
∴b>0,
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴abc<0,故A正确;
∵当x=1时,函数有最大值,
∴当m≠1时,a+b>am2+bm,故B正确;
∵ax12+bx1=ax22+bx2,
∴抛物线和x轴的交点坐标为(x1,0),(x2,0),
由图象可得x1+x2<3,故D错误;
故选D.
点评 本题考查了二次函数与系数的关系:对于二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右.常数项c决定抛物线与y轴交点:抛物线与y轴交于(0,c).


 小学教材全测系列答案
小学教材全测系列答案科目:初中数学 来源: 题型:解答题
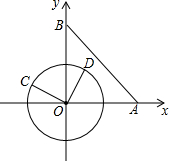 在平面直角坐标系xOy中,已知点A(6,0)、点B(0,6),动点C在以半径为3的⊙O上,连接OC,过O点作OD⊥OC,OD与⊙O相交于点D(其中点C、O、D按逆时针方向排列)连接AB
在平面直角坐标系xOy中,已知点A(6,0)、点B(0,6),动点C在以半径为3的⊙O上,连接OC,过O点作OD⊥OC,OD与⊙O相交于点D(其中点C、O、D按逆时针方向排列)连接AB查看答案和解析>>
科目:初中数学 来源: 题型:选择题
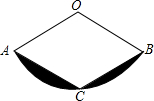 如图,扇形AOB中,OA=2,C为$\widehat{AB}$上的一点,连接AC,BC,如果四边形AOBC为菱形,则图中阴影部分的面积为( )
如图,扇形AOB中,OA=2,C为$\widehat{AB}$上的一点,连接AC,BC,如果四边形AOBC为菱形,则图中阴影部分的面积为( )| A. | $\frac{2π}{3}$-$\sqrt{3}$ | B. | $\frac{2π}{3}$-2$\sqrt{3}$ | C. | $\frac{4π}{3}$-$\sqrt{3}$ | D. | $\frac{4π}{3}$-2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
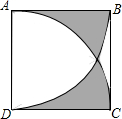 如图,正方形ABCD的边长为1,分别以A、D为圆心,1为半径画弧BD、AC,则图中阴影部分的面积$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$.
如图,正方形ABCD的边长为1,分别以A、D为圆心,1为半径画弧BD、AC,则图中阴影部分的面积$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com