Question

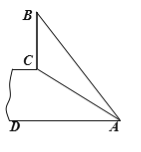
【题目】如图，斜坡AC的坡度（坡比）为1: ，AC＝10米．坡顶有一垂直于水平面的旗杆BC，旗杆顶端B点与A点有一条彩带AB相连，AB＝14米．试求旗杆BC的高度．

Answer 1

【答案】6米.

【解析】

试题分析：如果延长BC交AD于E点，则CE⊥AD，要求BC的高度，就要知道BE和CE的高度，就要先求出AE的长度．直角三角形ACE中有坡比，由AC的长，那么就可求出AE的长，然后求出BE、CE的高度，BC=BE-CE，即可得出结果．

试题解析：延长BC交AD于E点，则CE⊥AD．

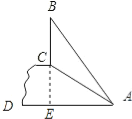
在Rt△AEC中，AC=10，由坡比为1：可知：∠CAE=30°，

∴CE=ACsin30°=10×=5，

AE=ACcos30°=10×=5．

在Rt△ABE中，．

∵BE=BC+CE，

∴BC=BE-CE=11-5=6（米）．

答：旗杆的高度为6米.

考点: 解直角三角形的应用-坡度坡角问题．