
分析 (1)把A点代入,根据待定系数法即可求得;
(2)作AC⊥x轴于C,BD⊥x轴于D,通过证得△APC∽△BPD,得出$\frac{AC}{BD}$=$\frac{AP}{PB}$=2,求得B的纵坐标,代入解析式求得坐标,然后根据待定系数法求得直线AB的解析式,令y=0,即可求得P的坐标.
解答 解:(1)∵反比例函数y=$\frac{m}{x}$的图象过点A(1,6),
∴k=1×6=6,
∴反比例函数的表达式为:y=$\frac{6}{x}$;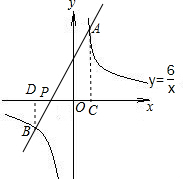
(2)作AC⊥x轴于C,BD⊥x轴于D,
∵AC∥BD,
∴△APC∽△BPD,
∴$\frac{AC}{BD}$=$\frac{AP}{PB}$,
∵AP=2PB,
∴AC=2BD,
∵AC=6,
∴BD=3,
∴B的纵坐标为±3,
把y=3代入y=$\frac{6}{x}$得3=$\frac{6}{x}$,解得x=2,
把y=-3代入y=$\frac{6}{x}$得,-3=$\frac{6}{x}$,解得x=-2,
∴B(2,3)或(-2,-3),
设直线AB的解析式为y=kx+b,
把A(1,6),B(2,3)代入得$\left\{\begin{array}{l}{k+b=6}\\{2k+b=3}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-3}\\{b=9}\end{array}\right.$
把A(1,6),B(-2,-3)代入得$\left\{\begin{array}{l}{k+b=6}\\{-2k+b=-3}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=3}\\{b=3}\end{array}\right.$,
∴直线AB的解析式为y=-3x+9或y=3x+3,
令y=0,则求得x=3或-1,
∴P的坐标为(3,0)或(-1,0).
点评 本题考查了反比例函数与一次函数的交点及待定系数法求函数解析式,待定系数法求函数解析式是本题的关键.


科目:初中数学 来源: 题型:选择题
 石墨烯(Graphene)是从石墨材料中剥离出来、由碳原子组成的只有一层原子厚度的二维晶体.石墨烯一层层叠起来就是石墨,厚1毫米的石墨大约包含300万层石墨烯.300万用科学记数法表示为( )
石墨烯(Graphene)是从石墨材料中剥离出来、由碳原子组成的只有一层原子厚度的二维晶体.石墨烯一层层叠起来就是石墨,厚1毫米的石墨大约包含300万层石墨烯.300万用科学记数法表示为( )| A. | 300×104 | B. | 3×105 | C. | 3×106 | D. | 3000000 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-2,0) | B. | (0,0) | C. | (-1,-1) | D. | (-2,-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{x+1}$ | B. | $-\frac{1}{x+1}$ | C. | $-\frac{1}{x-1}$ | D. | $\frac{1}{x-1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
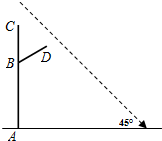 如图,铜亭广场装有智能路灯,路灯设备由灯柱AC与支架BD共同组成(点C处装有安全监控,点D处装有照明灯),灯柱AC为6米,支架BD为2米,支点B到A的距离为4米,AC与地面垂直,∠CBD=60°.某一时刻,太阳光与地面的夹角为45°,求此刻路灯设备在地面上的影长为多少?
如图,铜亭广场装有智能路灯,路灯设备由灯柱AC与支架BD共同组成(点C处装有安全监控,点D处装有照明灯),灯柱AC为6米,支架BD为2米,支点B到A的距离为4米,AC与地面垂直,∠CBD=60°.某一时刻,太阳光与地面的夹角为45°,求此刻路灯设备在地面上的影长为多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com