
ЁОЬтФПЁПдкЕШБп![]() жаЃЌЕу
жаЃЌЕу![]() ЮЊ
ЮЊ![]() ЩЯвЛЕуЃЌСЌНг
ЩЯвЛЕуЃЌСЌНг![]() ЃЌжБЯп
ЃЌжБЯп![]() гы
гы![]() ЗжБ№ЯрНЛгкЕу
ЗжБ№ЯрНЛгкЕу![]() ЃЌЧв
ЃЌЧв![]() ЃЎ
ЃЎ
ЃЈ1ЃЉШчЭМЃЈ1ЃЉЃЌаДГіЭМжаЫљгагы![]() ЯрЫЦЕФШ§НЧаЮЃЌВЂбЁдёЦфжаЕФвЛЖдИјгшжЄУїЃЛ
ЯрЫЦЕФШ§НЧаЮЃЌВЂбЁдёЦфжаЕФвЛЖдИјгшжЄУїЃЛ
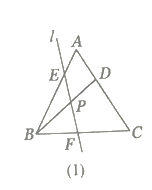
ЃЈ2ЃЉШєжБЯп![]() ЯђгвЦНвЦЕНЭМЃЈ2ЃЉЁЂЭМЃЈ3ЃЉЕФЮЛжУЪБЃЌЦфЫћЬѕМўВЛБфЃЌЃЈ1ЃЉжаЕФНсТлЪЧЗёШдШЛГЩСЂ?ШєГЩСЂЧыаДГіРД(ВЛжЄУї)ЃЌШєВЛГЩСЂЃЌЧыЫЕУїРэгЩЃЛ
ЯђгвЦНвЦЕНЭМЃЈ2ЃЉЁЂЭМЃЈ3ЃЉЕФЮЛжУЪБЃЌЦфЫћЬѕМўВЛБфЃЌЃЈ1ЃЉжаЕФНсТлЪЧЗёШдШЛГЩСЂ?ШєГЩСЂЧыаДГіРД(ВЛжЄУї)ЃЌШєВЛГЩСЂЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЬНОП:ШчЭМЃЈ1ЃЉЃЌЕБ![]() ТњзуЪВУДЬѕМўЪБ(ЦфЫћЬѕМўВЛБф)ЃЌ
ТњзуЪВУДЬѕМўЪБ(ЦфЫћЬѕМўВЛБф)ЃЌ![]() ?ЧыаДГіЬНОПНсЙћЃЌВЂЫЕУїРэгЩ(ЫЕУї:НсТлжаВЛЕУКЌгаЮДБъЪЖЕФзжФИ)ЃЎ
?ЧыаДГіЬНОПНсЙћЃЌВЂЫЕУїРэгЩ(ЫЕУї:НсТлжаВЛЕУКЌгаЮДБъЪЖЕФзжФИ)ЃЎ
ЁОД№АИЁПЃЈ1ЃЉ ЁїBPFЁзЁїEBFЃЌЁїBPFЁзЁїBCDЃЛЃЈ2ЃЉОљГЩСЂЃЌЗжБ№ЮЊЁїBPFЁзЁїEBFЃЌЁїBPFЁзЁїBCDЃЌЃЈ3ЃЉЕБBDЦНЗжЁЯABCЪБЃЌPF=![]() PEЃЎ
PEЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩСННЧЖдгІЯрЕШЕФШ§НЧаЮЪЧЯрЫЦШ§НЧаЮевГіЁїBPFЁзЁїEBFЃЌЁїBPFЁзЁїBCDЃЌетСНзщШ§НЧаЮЖМПЩгЩвЛИіЙЋЙВНЧКЭвЛзщ60ЁуНЧРДжЄУїЃЛ
ЃЈ2ЃЉГЩСЂЃЌжЄЗЈЭЌЃЈ1ЃЉЃЛ
ЃЈ3ЃЉЯШПДPF=![]() PEФмЕУГіЪВУДНсТлЃЌИљОнЁїBPFЁзЁїEBFЃЌПЩЕУBF2=PFPE=3PF2ЃЌвђДЫ
PEФмЕУГіЪВУДНсТлЃЌИљОнЁїBPFЁзЁїEBFЃЌПЩЕУBF2=PFPE=3PF2ЃЌвђДЫ![]() ЃЌвђЮЊ
ЃЌвђЮЊ![]() ЃЌПЩЕУЁЯPFB=90ЁуЃЌдђЁЯPBF=30ЁуЃЌгЩДЫПЩЕУЕБBDЦНЗжЁЯABCЪБЃЌPF=
ЃЌПЩЕУЁЯPFB=90ЁуЃЌдђЁЯPBF=30ЁуЃЌгЩДЫПЩЕУЕБBDЦНЗжЁЯABCЪБЃЌPF=![]() PEЃЎ
PEЃЎ
НтЃКЃЈ1ЃЉЁїBPFЁзЁїEBFЃЌЁїBPFЁзЁїBCDЃЌжЄУїШчЯТЃК
ЁпЁїABCЪЧЕШБпШ§НЧаЮЃЌ
ЁрЁЯABC=ЁЯACB=ЁЯBAC=60ЁуЃЌ
ЁпЁЯBPF=60Ёу
ЁрЁЯBPF=ЁЯEBF=60ЁуЃЌ
ЁпЁЯBFP=ЁЯBFEЃЌ
ЁрЁїBPFЁзЁїEBFЃЛ
ЁпЁЯBPF=ЁЯBCD=60ЁуЃЌЁЯPBF=ЁЯCBDЃЌ
ЁрЁїBPFЁзЁїBCDЃЛ
ЃЈ2ЃЉОљГЩСЂЃЌЗжБ№ЮЊЁїBPFЁзЁїEBFЃЌЁїBPFЁзЁїBCDЃЌжЄУїШчЯТЃК
ШчЭМЃЈ2ЃЉЁпЁЯBPF=ЁЯEBF=60ЁуЃЌЁЯBFP=ЁЯBFEЃЌ
ЁрЁїBPFЁзЁїEBFЃЛ
ЁпЁЯBPF=ЁЯBCD=60ЁуЃЌЁЯPBF=ЁЯCBDЃЌ
ЁрЁїBPFЁзЁїBCDЃЎ
ШчЭМЃЈ3ЃЉЃЌЭЌРэПЩжЄЁїBPFЁзЁїEBFЃЌЁїBPFЁзЁїBCDЃЛ
ЃЈ3ЃЉЕБBDЦНЗжЁЯABCЪБЃЌPF=![]() PEЃЌ
PEЃЌ
РэгЩЃКЁпBDЦНЗжЁЯABCЃЌЁрЁЯABP=ЁЯPBF=30ЁуЃЎ
ЁпЁЯBPF=60ЁуЃЌЁрЁЯBFP=90ЁуЃЎ
ЁрPF=![]() PB
PB
гжЁпЁЯBEF=60Ёу30Ёу=30Ёу=ЁЯABPЃЌ
ЁрPB=PEЃЎ
ЁрPF=![]() PEЃЎ
PEЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСЯТУцВФСЯЃК
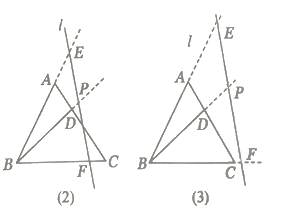
бЇЯАКЏЪ§жЊЪЖКѓЃЌЖдгквЛаЉЬиЪтЕФВЛЕШЪНЃЌЮвУЧПЩвдНшжњКЏЪ§ЭМЯѓРДЧѓГіЫќЕФНтМЏЃЌР§ШчЧѓВЛЕШЪНxЉ3ЃО![]() ЕФНтМЏЃЌЮвУЧПЩвддкЭЌвЛзјБъЯЕжаЃЌЛГіжБЯпy1ЃНxЉ3гыКЏЪ§y2ЃН
ЕФНтМЏЃЌЮвУЧПЩвддкЭЌвЛзјБъЯЕжаЃЌЛГіжБЯпy1ЃНxЉ3гыКЏЪ§y2ЃН![]() ЕФЭМЯѓЃЈШчЭМ1ЃЉЃЌЙлВьЭМЯѓПЩжЊЃКЫќУЧНЛгкЕуAЃЈЉ1ЃЌЉ4ЃЉЃЌBЃЈ4ЃЌ1ЃЉЃЎЕБЉ1ЃМxЃМ0ЃЌЛђxЃО4ЪБЃЌy1ЃОy2ЃЌМДВЛЕШЪНxЉ3ЃО
ЕФЭМЯѓЃЈШчЭМ1ЃЉЃЌЙлВьЭМЯѓПЩжЊЃКЫќУЧНЛгкЕуAЃЈЉ1ЃЌЉ4ЃЉЃЌBЃЈ4ЃЌ1ЃЉЃЎЕБЉ1ЃМxЃМ0ЃЌЛђxЃО4ЪБЃЌy1ЃОy2ЃЌМДВЛЕШЪНxЉ3ЃО![]() ЕФНтМЏЮЊЉ1ЃМxЃМ0ЃЌЛђxЃО4ЃЎ
ЕФНтМЏЮЊЉ1ЃМxЃМ0ЃЌЛђxЃО4ЃЎ
аЁЖЋИљОнбЇЯАвдЩЯжЊЪЖЕФОбщЃЌЖдЧѓВЛЕШЪНx3+3x2ЉxЉ3ЃО0ЕФНтМЏНјааСЫЬНОПЃЎЯТУцЪЧаЁЖЋЕФЬНОПЙ§ГЬЃЌЧыВЙГфЭъећЃК
ЃЈ1ЃЉНЋВЛЕШЪНАДЬѕМўНјаазЊЛЏЃКЕБxЃН0ЪБЃЌдВЛЕШЪНВЛГЩСЂЃЛxЃО0ЪБЃЌдВЛЕШЪНзЊЛЏЮЊx2+3xЉ1ЃО![]() ЃЛЕБxЃМ0ЪБЃЌдВЛЕШЪНзЊЛЏЮЊ______ЃЛ
ЃЛЕБxЃМ0ЪБЃЌдВЛЕШЪНзЊЛЏЮЊ______ЃЛ
ЃЈ2ЃЉЙЙдьКЏЪ§ЃЌЛГіЭМЯѓЃКЩшy3ЃНx2+3xЉ1ЃЌy4ЃН![]() ЃЌдкЭЌвЛзјБъЯЕЃЈЭМ2ЃЉжаЗжБ№ЛГіетСНИіКЏЪ§ЕФЭМЯѓЃЎ
ЃЌдкЭЌвЛзјБъЯЕЃЈЭМ2ЃЉжаЗжБ№ЛГіетСНИіКЏЪ§ЕФЭМЯѓЃЎ
ЃЈ3ЃЉНшжњЭМЯѓЃЌаДГіНтМЏЃКЙлВьЫљЛСНИіКЏЪ§ЕФЭМЯѓЃЌШЗЖЈСНИіКЏЪ§ЭМЯѓНЛЕуЕФКсзјБъЃЌНсКЯЃЈ1ЃЉЕФЬжТлНсЙћЃЌПЩжЊЃКВЛЕШЪНx3+3x2ЉxЉ3ЃО0ЕФНтМЏЮЊ______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
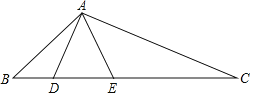
ЁОЬтФПЁПШчЭМЃЌвбжЊдкЁїABCжаЃЌЕуDЁЂЕуEдкBCБпЩЯЃЌЧв![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїABDЁзЁїCBAЃЎ
ЃЈ2ЃЉШєЁїACEЁзЁїBCAЃЌХаЖЈЁїADEЕФаЮзДЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉдкЃЈ1ЃЉКЭЃЈ2ЃЉЕФЬѕМўЯТЃЌШєtanЁЯADCЃН2ЃЌDEЃН6ЃЌЧыЧѓГіAEЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЪЬтЃКШчЭМ1ЃЌЁїABCжаЃЌABЃНaЃЌЁЯACBЃНІСЃЎШчКЮгУжБГпКЭдВЙцзїГіЕуPЃЌОљЪЙЕУЁЯAPBЃН![]() ІСЃПЃЈВЛашНтД№ЃЉ
ІСЃПЃЈВЛашНтД№ЃЉ
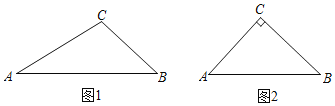
ГЂЪдЃКШчЭМ2ЃЌЁїABCжаЃЌACЃНBCЃЌЁЯACBЃН90ЁуЃЎ
ЃЈ1ЃЉЧыгУжБНЧШ§НЧГпЃЈНіПЩЛжБНЧЛђжБЯпЃЉдкЭМ2жаЛГівЛИіЕуPЃЌЪЙЕУЁЯAPBЃН45Ёу
ЃЈ2ЃЉШчЭМ3ЃЌШєACЃНBCЃН![]() ЃЌвдЕуAЮЊдЕуЃЌжБЯпABЮЊxжсЃЌЙ§ЕуAДЙжБгкABЕФжБЯпЮЊyжсНЈСЂЦНУцжБНЧзјБъЯЕЃЌжБЯпyЃН
ЃЌвдЕуAЮЊдЕуЃЌжБЯпABЮЊxжсЃЌЙ§ЕуAДЙжБгкABЕФжБЯпЮЊyжсНЈСЂЦНУцжБНЧзјБъЯЕЃЌжБЯпyЃН![]() ЃЈbЁн0ЃЉНЛxжсгкЕуMЃЌНЛyжсгыЕуNЃЎ
ЃЈbЁн0ЃЉНЛxжсгкЕуMЃЌНЛyжсгыЕуNЃЎ
ЂйЕБbЃН7+![]() ЪБЃЌЧыНігУдВЙцдкЩфЯпMNЩЯзїГіЕуPЃЌЪЙЕУЁЯAPBЃН45ЁуЃЛ
ЪБЃЌЧыНігУдВЙцдкЩфЯпMNЩЯзїГіЕуPЃЌЪЙЕУЁЯAPBЃН45ЁуЃЛ
ЂкЧыжБНгаДГіЩфЯпMNЩЯЪЙЕУЁЯAPBЃН45ЁуЛђЁЯAPBЃН135ЁуЪБЕуPЕФИіЪ§МАЯргІЕФbЕФШЁжЕЗЖЮЇЃЛ
ЂлгІгУЃКШчЭМ4ЃЌЁїABCжаЃЌABЃНaЃЌЁЯACBЃНІСЃЌЧыгУжБГпКЭдВЙцзїГіЕуPЃЌЪЙЕУЁЯAPBЃНІСЃЌЧвAP+BPзюДѓЃЌЧыМђвЊЫЕУїРэгЩЃЎЃЈВЛаДзїЗЈЃЌБЃСєзїЭМКлМЃЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
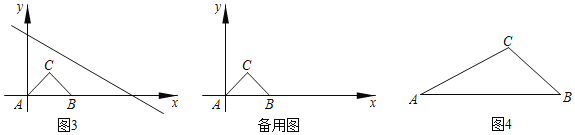
ЁОЬтФПЁПвбжЊЃКЁїABCдкжБНЧзјБъЦНУцФкЃЌШ§ИіЖЅЕуЕФзјБъЗжБ№ЮЊAЃЈ0ЃЌ3ЃЉЁЂBЃЈ3ЃЌ4ЃЉЁЂCЃЈ2ЃЌ2ЃЉЃЈе§ЗНаЮЭјИёжаУПИіаЁе§ЗНаЮЕФБпГЄЪЧвЛИіЕЅЮЛГЄЖШЃЉЃЎ
ЃЈ1ЃЉЛГіЁїABCЯђЯТЦНвЦ4ИіЕЅЮЛГЄЖШЕУЕНЕФЁїA1B1C1ЃЌЕуC1ЕФзјБъЪЧЁЁ ЁЁЃЛ
ЃЈ2ЃЉвдЕуBЮЊЮЛЫЦжааФЃЌдкЭјИёФкЛГіЁїA2B2C2ЃЌЪЙЁїA2B2C2гыЁїABCЮЛЫЦЃЌЧвЮЛЫЦБШЮЊ2ЃК1ЃЌЕуC2ЕФзјБъЪЧЁЁ ЁЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
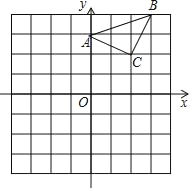
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌ![]() ЮЊзјБъдЕуЃЌ
ЮЊзјБъдЕуЃЌ![]() ЕФБп
ЕФБп![]() ДЙжБгк
ДЙжБгк![]() жсЁЂДЙзуЮЊЕу
жсЁЂДЙзуЮЊЕу![]() ЃЌЗДБШР§КЏЪ§
ЃЌЗДБШР§КЏЪ§![]() ЕФЭМЯѓОЙ§
ЕФЭМЯѓОЙ§![]() ЕФжаЕу
ЕФжаЕу![]() ЁЂЧвгы
ЁЂЧвгы![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЎОЙ§
ЃЎОЙ§![]() ЁЂ
ЁЂ![]() СНЕуЕФвЛДЮКЏЪ§НтЮіЪНЮЊ
СНЕуЕФвЛДЮКЏЪ§НтЮіЪНЮЊ![]() ЃЌШєЕу
ЃЌШєЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌ
ЃЌ![]() ЃЎЧв
ЃЎЧв![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓЗДБШР§КЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉдкжБЯп![]() ЩЯгавЛЕу
ЩЯгавЛЕу![]() ЃЌ
ЃЌ![]() ЕФУцЛ§ЕШгк
ЕФУцЛ§ЕШгк![]() ЃЎЧѓТњзуЬѕМўЕФЕу
ЃЎЧѓТњзуЬѕМўЕФЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ3ЃЉЧыЙлВьЭМЯѓжБНгаДГіВЛЕШЪН![]() ЕФНтМЏЃЎ
ЕФНтМЏЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩЬГЁЯњЪлФГжжБљЯфЃЌИУжжБљЯфУПЬЈНјМлЮЊ2500дЊЃЌвбжЊдЯњЪлМлЮЊУПЬЈ2900дЊЪБЃЌЦНОљУПЬьФмЪлГі8ЬЈЃЎШєдкдЯњЪлМлЕФЛљДЁЩЯУПЬЈНЕМл50дЊЃЌдђЦНОљУПЬьПЩЖрЪлГі4ЬЈЃЎЩшУПЬЈБљЯфЕФЪЕМЪЪлМлБШдЯњЪлМлНЕЕЭСЫ![]() дЊЃЎ
дЊЃЎ
ЃЈ1ЃЉЬюБэЃК
УПЬьЕФЯњЪлСП/ЬЈ | УПЬЈЯњЪлРћШѓ/дЊ | |
НЕМлЧА | 8 | 400 |
НЕМлКѓ |
ЃЈ2ЃЉЩЬГЁЮЊЪЙетжжБљЯфЦНОљУПЬьЕФЯњЪлРћШѓДяЕНзюДѓЪБЃЌдђУПЬЈБљЯфЕФЪЕМЪЪлМлгІЖЈЮЊЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПСтаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЪЧЖдНЧЯп
ЪЧЖдНЧЯп![]() ЫљдкжБЯпЩЯвЛЕуЃЌЧв
ЫљдкжБЯпЩЯвЛЕуЃЌЧв![]() ЃЌжБЯп
ЃЌжБЯп![]() НЛжБЯп
НЛжБЯп![]() гкЕу
гкЕу![]() ЃЌдђ
ЃЌдђ![]() ____________
____________
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
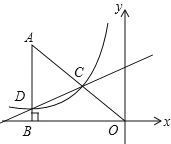
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊХзЮяЯпy=x2+bx+cЙ§AЃЌBЃЌCШ§ЕуЃЌЕуAЕФзјБъЪЧЃЈ3ЃЌ0ЃЉЃЌЕуCЕФзјБъЪЧЃЈ0ЃЌ-3ЃЉЃЌЖЏЕуPдкХзЮяЯпЩЯЃЎ
ЃЈ1ЃЉb =_________ЃЌc =_________ЃЌЕуBЕФзјБъЮЊ_____________ЃЛЃЈжБНгЬюаДНсЙћЃЉ
ЃЈ2ЃЉЪЧЗёДцдкЕуPЃЌЪЙЕУЁїACPЪЧвдACЮЊжБНЧБпЕФжБНЧШ§НЧаЮЃПШєДцдкЃЌЧѓГіЫљгаЗћКЯЬѕМўЕФЕуPЕФзјБъЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЙ§ЖЏЕуPзїPEДЙжБyжсгкЕуEЃЌНЛжБЯпACгкЕуDЃЌЙ§ЕуDзїxжсЕФДЙЯпЃЎДЙзуЮЊFЃЌСЌНгEFЃЌЕБЯпЖЮEFЕФГЄЖШзюЖЬЪБЃЌЧѓГіЕуPЕФзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com