
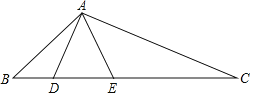
【题目】如图,已知在△ABC中,点D、点E在BC边上,且![]() .
.
(1)求证:△ABD∽△CBA.
(2)若△ACE∽△BCA,判定△ADE的形状,并说明理由;
(3)在(1)和(2)的条件下,若tan∠ADC=2,DE=6,请求出AE的长.
【答案】(1)详见解析;(2)△ADE是等腰三角形,理由详见解析;(3)3![]() .
.
【解析】
(1)根据两边成比例夹角相等两三角形相似即可证明.
(2)结论:△ADE是等腰三角形.理由相似三角形的性质证明∠ADE=∠AED即可.
(3)作AH⊥DE于H.解直角三角形求出AD即可解决问题.
(1)证明:∵![]() ,∠B=∠B,
,∠B=∠B,
∴△ABD∽△CBA.
(2)结论:△ADE是等腰三角形.
理由:∵△ACE∽△BCA,
∴∠AEC=∠BAC,
∵△ABD∽△CBA,
∴∠BAC=∠BDA,
∴∠BDA=∠CEA,
∴AD=AE,
∴△ADE是等腰三角形.
(3)如图,作AH⊥DE于H.
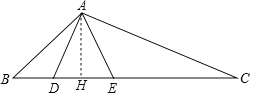
∵AD=AE,AH⊥DE,
∴DH=HE=![]() DE=3,
DE=3,
∵tan∠ADE=![]() =2,
=2,
∴AH=6,
∴AD=AE=![]() =3
=3![]() .
.


科目:初中数学 来源: 题型:
【题目】小红想利用阳光下的影长测量学校旗杆AB的高度.如图,他在某一时刻在地面上竖直立一个2米长的标杆CD,测得其影长DE=0.4米.

(1)请在图中画出此时旗杆AB在阳光下的投影BF.
(2)如果BF=1.6,求旗杆AB的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2015德阳)大华服装厂生产一件秋冬季外套需面料1.2米,里料0.8米,已知面料的单价比里料的单价的2倍还多10元,一件外套的布料成本为76元.
(1)求面料和里料的单价;
(2)该款外套9月份投放市场的批发价为150元/件,出现购销两旺态势,10月份进入批发淡季,厂方决定采取打折促销.已知生产一件外套需人工等固定费用14元,为确保每件外套的利润不低于30元.
①设10月份厂方的打折数为m,求m的最小值;(利润=销售价﹣布料成本﹣固定费用)
②进入11月份以后,销售情况出现好转,厂方决定对VIP客户在10月份最低折扣价的基础上实施更大的优惠,对普通客户在10月份最低折扣价的基础上实施价格上浮.已知对VIP客户的降价率和对普通客户的提价率相等,结果一个VIP客户用9120元批发外套的件数和一个普通客户用10080元批发外套的件数相同,求VIP客户享受的降价率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司从2014年开始投入技术改进资金,经技术改进后,其产品的成本不断降低,具体数据如下表:
年 度 | 2013 | 2014 | 2015 | 2016 |
投入技改资金 | 2.5 | 3 | 4 | 4.5 |
产品成本 | 7.2 | 6 | 4.5 | 4 |
(1)请你认真分析表中数据,从一次函数和反比例函数中确定哪一个函数能表示其变化规律,给出理由,并求出其解析式;
(2)按照这种变化规律,若2017年已投入资金5万元.
①预计生产成本每件比2016年降低多少万元?
②若打算在2017年把每件产品成本降低到3.2万元,则还需要投入技改资金多少万元?(结果精确到0.01万元).
查看答案和解析>>
科目:初中数学 来源: 题型:
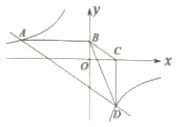
【题目】如图,反比例函数![]() 的图象经过点
的图象经过点![]() ,直线
,直线![]() 与双曲线交于另一点
与双曲线交于另一点![]() ,作
,作![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,连接
,连接![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() ,求直线
,求直线![]() 的解析式;
的解析式;
(3)若![]() ,其它条件不变,直接写出
,其它条件不变,直接写出![]() 与
与![]() 的位置关系.
的位置关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读小明用下面的方法求出方程2![]() ﹣3x=0的
﹣3x=0的
解法1:令 原方程化为2t﹣3t2=0 解方程2t﹣3t2=0,得t1=0,t2= 所以 将方程 得x=0或 经检验,x=0或 所以,原方程的解是x=0或 | 解法2:移项,得2 方程两边同时平方,得4x=9x2, 解方程4x=9x2,得x=0或 经检验,x=0或 所以,原方程的解是x=0或 |
请仿照他的某一种方法,求出方法x﹣![]() =﹣1的解.
=﹣1的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
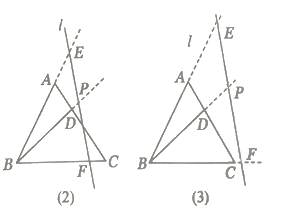
【题目】在等边![]() 中,点
中,点![]() 为
为![]() 上一点,连接
上一点,连接![]() ,直线
,直线![]() 与
与![]() 分别相交于点
分别相交于点![]() ,且
,且![]() .
.
(1)如图(1),写出图中所有与![]() 相似的三角形,并选择其中的一对给予证明;
相似的三角形,并选择其中的一对给予证明;
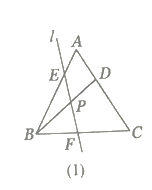
(2)若直线![]() 向右平移到图(2)、图(3)的位置时,其他条件不变,(1)中的结论是否仍然成立?若成立请写出来(不证明),若不成立,请说明理由;
向右平移到图(2)、图(3)的位置时,其他条件不变,(1)中的结论是否仍然成立?若成立请写出来(不证明),若不成立,请说明理由;
(3)探究:如图(1),当![]() 满足什么条件时(其他条件不变),
满足什么条件时(其他条件不变),![]() ?请写出探究结果,并说明理由(说明:结论中不得含有未标识的字母).
?请写出探究结果,并说明理由(说明:结论中不得含有未标识的字母).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象相交于A(2,2),B(n,4)两点,连接OA、OB.
的图象相交于A(2,2),B(n,4)两点,连接OA、OB.
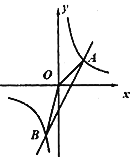
(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积;
(3)在直角坐标系中,是否存在一点P,使以P、A、O、B为顶点的四边形是平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com