
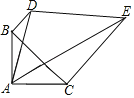
【题目】如图,△ABC中,AB=AC,∠BAC=90°,BD⊥BC,CE⊥BC,∠DAE=45°,若BD=![]() ,CE=3
,CE=3![]() ,则线段DE=_____.
,则线段DE=_____.
【答案】10.
【解析】
将△ABD绕点A顺时针旋转90°得到△ACF,连接EF,则CF=BD=![]() ,AF=AD,∠CAF=∠BAD,易证∠DBC=∠ECB=90°,由等腰直角三角形的性质得出∠ABC=∠ACB=45°,推出∠ABD=∠ACF=∠ACE=135°,得出∠ECF=90°,由勾股定理得出EF=
,AF=AD,∠CAF=∠BAD,易证∠DBC=∠ECB=90°,由等腰直角三角形的性质得出∠ABC=∠ACB=45°,推出∠ABD=∠ACF=∠ACE=135°,得出∠ECF=90°,由勾股定理得出EF=![]() =10,证明∠EAD=∠EAF,由SAS证得△EAF≌△EAD,即可得出结果.
=10,证明∠EAD=∠EAF,由SAS证得△EAF≌△EAD,即可得出结果.
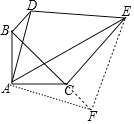
将△ABD绕点A顺时针旋转90°得到△ACF,连接EF,如图所示:
则CF=BD=![]() ,AF=AD,∠CAF=∠BAD,
,AF=AD,∠CAF=∠BAD,
∵BD⊥BC,EC⊥BC,
∴∠DBC=∠ECB=90°,
∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°,
∴∠ABD=∠ACF=∠ACE=135°,
∴∠ECF=90°,
在Rt△ECF中,EF=![]() =
=![]() =10,
=10,
∵∠DAE=45°,
∴∠EAF=∠EAC+∠CAF=∠EAC+∠BAD=45°,
∴∠EAD=∠EAF,
在△EAF和△EAD中, ,
,
∴△EAF≌△EAD(SAS),
∴DE=EF=10,
故答案为:10.


科目:初中数学 来源: 题型:
【题目】某水果公司新购进10000千克柑橘,每千克柑橘的成本为9元. 柑橘在运输、存储过程中会有损坏,销售人员从所有的柑橘中随机抽取若干柑橘,进行“柑橘损坏率”统计,并把获得的数据记录如下:
柑橘总重量n/千克 | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 |
损坏柑橘重量m/千克 | 5.50 | 10.50 | 15.15 | 19.42 | 24.25 | 30.93 | 35.32 | 39.24 | 44.57 | 51.54 |
柑橘损坏的频率 | 0.110 | 0.105 | 0.101 | 0.097 | 0.097 | 0.103 | 0.101 | 0.098 | 0.099 | 0.103 |
根据以上数据,估计柑橘损坏的概率为 (结果保留小数点后一位);由此可知,去掉损坏的柑橘后,水果公司为了不亏本,完好柑橘每千克的售价至少为________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
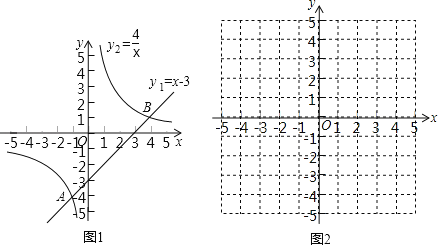
学习函数知识后,对于一些特殊的不等式,我们可以借助函数图象来求出它的解集,例如求不等式x﹣3>![]() 的解集,我们可以在同一坐标系中,画出直线y1=x﹣3与函数y2=
的解集,我们可以在同一坐标系中,画出直线y1=x﹣3与函数y2=![]() 的图象(如图1),观察图象可知:它们交于点A(﹣1,﹣4),B(4,1).当﹣1<x<0,或x>4时,y1>y2,即不等式x﹣3>
的图象(如图1),观察图象可知:它们交于点A(﹣1,﹣4),B(4,1).当﹣1<x<0,或x>4时,y1>y2,即不等式x﹣3>![]() 的解集为﹣1<x<0,或x>4.
的解集为﹣1<x<0,或x>4.
小东根据学习以上知识的经验,对求不等式x3+3x2﹣x﹣3>0的解集进行了探究.下面是小东的探究过程,请补充完整:
(1)将不等式按条件进行转化:当x=0时,原不等式不成立;x>0时,原不等式转化为x2+3x﹣1>![]() ;当x<0时,原不等式转化为______;
;当x<0时,原不等式转化为______;
(2)构造函数,画出图象:设y3=x2+3x﹣1,y4=![]() ,在同一坐标系(图2)中分别画出这两个函数的图象.
,在同一坐标系(图2)中分别画出这两个函数的图象.
(3)借助图象,写出解集:观察所画两个函数的图象,确定两个函数图象交点的横坐标,结合(1)的讨论结果,可知:不等式x3+3x2﹣x﹣3>0的解集为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD中,∠B=60°,点E在边BC上,∠BAE=25°,把线段AE绕点A逆时针方向旋转,使点E落在边CD上,那么旋转角![]() 的度数为______.
的度数为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
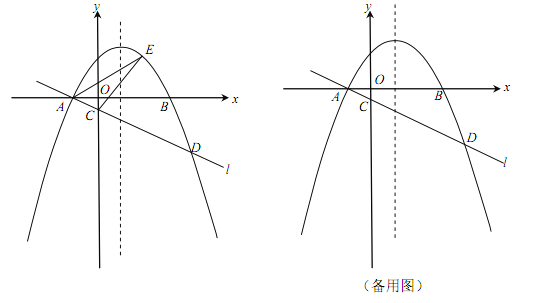
【题目】(本小题满分12分)如图,在平面直角坐标系xOy中,抛物线![]() (
(![]() )与x轴交于A,B两点(点A在点B的左侧),经过点A的直线l:
)与x轴交于A,B两点(点A在点B的左侧),经过点A的直线l:![]() 与y轴负半轴交于点C,与抛物线的另一个交点为D,且CD=4AC.
与y轴负半轴交于点C,与抛物线的另一个交点为D,且CD=4AC.
(1)直接写出点A的坐标,并求直线l的函数表达式(其中k,b用含a的式子表示);
(2)点E是直线l上方的抛物线上的动点,若△ACE的面积的最大值为![]() ,求a的值;
,求a的值;
(3)设P是抛物线的对称轴上的一点,点Q在抛物线上,以点A,D,P,Q为顶点的四边形能否成为矩形?若能,求出点P的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2﹣mx﹣m﹣1与x轴交于A、B两点,点A在点B的左边,与y轴交于点C(0,﹣3).
(1)求点A、B的坐标;
(2)点D是抛物线上一点,且∠ACO+∠BCD=45°,求点D的坐标;
(3)将抛物线向上平移m个单位,交线段BC于点M,N,若∠MON=45°,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
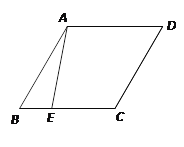
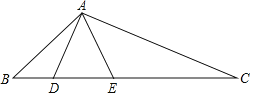
【题目】如图,已知在△ABC中,点D、点E在BC边上,且![]() .
.
(1)求证:△ABD∽△CBA.
(2)若△ACE∽△BCA,判定△ADE的形状,并说明理由;
(3)在(1)和(2)的条件下,若tan∠ADC=2,DE=6,请求出AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:如图1,△ABC中,AB=a,∠ACB=α.如何用直尺和圆规作出点P,均使得∠APB=![]() α?(不需解答)
α?(不需解答)
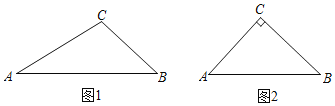
尝试:如图2,△ABC中,AC=BC,∠ACB=90°.
(1)请用直角三角尺(仅可画直角或直线)在图2中画出一个点P,使得∠APB=45°
(2)如图3,若AC=BC=![]() ,以点A为原点,直线AB为x轴,过点A垂直于AB的直线为y轴建立平面直角坐标系,直线y=
,以点A为原点,直线AB为x轴,过点A垂直于AB的直线为y轴建立平面直角坐标系,直线y=![]() (b≥0)交x轴于点M,交y轴与点N.
(b≥0)交x轴于点M,交y轴与点N.
①当b=7+![]() 时,请仅用圆规在射线MN上作出点P,使得∠APB=45°;
时,请仅用圆规在射线MN上作出点P,使得∠APB=45°;
②请直接写出射线MN上使得∠APB=45°或∠APB=135°时点P的个数及相应的b的取值范围;
③应用:如图4,△ABC中,AB=a,∠ACB=α,请用直尺和圆规作出点P,使得∠APB=α,且AP+BP最大,请简要说明理由.(不写作法,保留作图痕迹)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com