
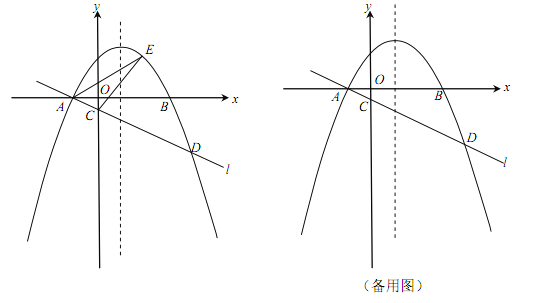
����Ŀ������С������12�֣���ͼ����ƽ��ֱ������ϵxOy�У�������![]() ��
��![]() ����x�ύ��A��B���㣨��A�ڵ�B����ࣩ��������A��ֱ��l��
����x�ύ��A��B���㣨��A�ڵ�B����ࣩ��������A��ֱ��l��![]() ��y�Ḻ���ύ�ڵ�C���������ߵ���һ������ΪD����CD=4AC��
��y�Ḻ���ύ�ڵ�C���������ߵ���һ������ΪD����CD=4AC��
��1��ֱ��д����A�����꣬����ֱ��l�ĺ�������ʽ������k��b�ú�a��ʽ�ӱ�ʾ����
��2����E��ֱ��l�Ϸ����������ϵĶ��㣬����ACE����������ֵΪ![]() ����a��ֵ��
����a��ֵ��
��3����P�������ߵĶԳ����ϵ�һ�㣬��Q���������ϣ��Ե�A��D��P��QΪ������ı����ܷ��Ϊ���Σ����ܣ������P�����ꣻ�����ܣ���˵�����ɣ�
���𰸡���1��A����1��0����![]() ����2��
����2��![]() ����3��P��������1��
����3��P��������1��![]() ����1����4����
����1����4����
��������
���⣨1����![]() �У���y=0���õ�
�У���y=0���õ�![]() ��
��![]() ���õ�A����1��0����B��3��0������ֱ��l������A���õ�
���õ�A����1��0����B��3��0������ֱ��l������A���õ�![]() ����
����![]() ����
����![]() ����
����![]() ������CD��4AC���ʵ�D�ĺ�����Ϊ4������
������CD��4AC���ʵ�D�ĺ�����Ϊ4������![]() ���õ�
���õ�![]() ���Ӷ��ó�ֱ��l�ĺ�������ʽ��
���Ӷ��ó�ֱ��l�ĺ�������ʽ��
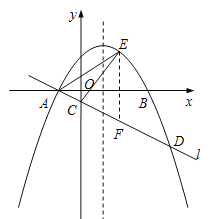
��2������E��EF��y�ᣬ��ֱ��l�ڵ�F����E��![]() ��
��![]() ������F��
������F��![]() ��
��![]() ����
����
EF��![]() =
=![]() ��S��ACE��S��AFE��S��CFE��
��S��ACE��S��AFE��S��CFE��![]() ��
��![]() ������ACE����������ֵΪ
������ACE����������ֵΪ![]() ������ACE����������ֵΪ
������ACE����������ֵΪ![]() ������
������![]() �����
�����![]() ��
��
��3����![]() ����
����![]() �����
�����![]() ��
��![]() ���õ�D��4��5a������Ϊ�����ߵĶԳ���Ϊ
���õ�D��4��5a������Ϊ�����ߵĶԳ���Ϊ![]() ����P��1��m����Ȼ�������������ۣ�����AD�Ǿ��ε�һ���ߣ�����AD�Ǿ��ε�һ���Խ��ߣ�
����P��1��m����Ȼ�������������ۣ�����AD�Ǿ��ε�һ���ߣ�����AD�Ǿ��ε�һ���Խ��ߣ�
�����������1����![]() =
=![]() ����y=0���õ�
����y=0���õ�![]() ��
��![]() ����A����1��0����B��3��0������ֱ��l������A����
����A����1��0����B��3��0������ֱ��l������A����![]() ��
��![]() ����
����![]() ����
����![]() ����
����![]() ����CD��4AC������D�ĺ�����Ϊ4����
����CD��4AC������D�ĺ�����Ϊ4����![]() ����
����![]() ����ֱ��l�ĺ�������ʽΪ
����ֱ��l�ĺ�������ʽΪ![]() ��
��
��2������E��EF��y�ᣬ��ֱ��l�ڵ�F����E��![]() ��
��![]() ������F��
������F��![]() ��
��![]() ����
����
EF��![]() =
=![]() ��
��
S��ACE��S��AFE��S��CFE��![]()
��![]() ��
��![]() ��
��
���ACE����������ֵΪ![]() ���ߡ�ACE����������ֵΪ
���ߡ�ACE����������ֵΪ![]() ����
����![]() �����
�����![]() ��
��
��3����![]() ����
����![]() �����
�����![]() ��
��![]() ����D��4��5a������
����D��4��5a������![]() ���������ߵĶԳ���Ϊ
���������ߵĶԳ���Ϊ![]() ����P��1��m����
����P��1��m����
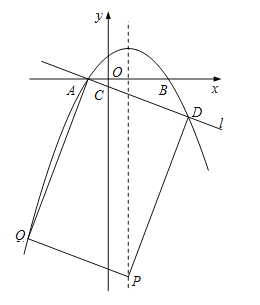
����AD�Ǿ��ε�һ���ߣ���Q����4��21a����m��21a��5a��26a����P��1��26a�������ı���ADPQΪ���Σ����ADP��90������![]() ����
����![]() ����
����![]() ����
����![]() ����
����![]() ����P1��1��
����P1��1��![]() ����
����
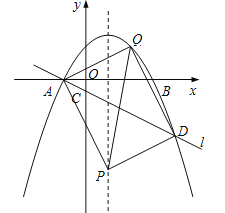
����AD�Ǿ��ε�һ���Խ��ߣ����߶�AD���е�����Ϊ��![]() ��
��![]() ����Q��2��
����Q��2��![]() ����m��
����m��![]() ����P��1��8a�������ı���APDQΪ���Σ����APD��90������
����P��1��8a�������ı���APDQΪ���Σ����APD��90������![]() ����
����![]() ����
����![]() ����
����![]() ����
����![]() ����P2��1����4����
����P2��1����4����
�����������Ե�A��D��P��QΪ������ı����ܳ�Ϊ���Σ���P������Ϊ��1��![]() ����1����4����
����1����4����


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ȫ��ͬ��С������ƴ����һ�����Σ�AB������һ��С�����εĶԽ��ߣ����ڴ�����������л�ͼ��Ҫ���������̶�ֱ�ߣ���������Ҫ�Ļ�ͼ�ۼ���
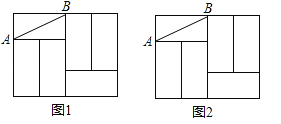
��1����ͼ1�л���һ��45���ǣ�ʹ��A���B������ǵĶ��㣬��ABΪ����ǵ�һ�ߣ�
��2����ͼ2�л����߶�AB�Ĵ�ֱƽ���ߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
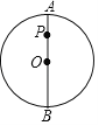
����Ŀ����ͼ��AB�ǡ�O��ֱ������P��AB��һ�㣬�ҵ�P����CD���е㣮
��1�������⻭����CD����˵����ͼ�����ݣ�����д������������ͼ�ۼ���
��2����AP��2��CD��8�����O�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2015��������װ������һ���ﶬ������������1.2�ף�����0.8�ף���֪���ϵĵ��۱����ϵĵ��۵�2������10Ԫ��һ�����IJ��ϳɱ�Ϊ76Ԫ��
��1�������Ϻ����ϵĵ��ۣ�
��2���ÿ�����9�·�Ͷ���г���������Ϊ150Ԫ/�������ֹ�������̬�ƣ�10�·ݽ�����������������������ȡ���۴�������֪����һ���������˹��ȹ̶�����14Ԫ��Ϊȷ��ÿ������������30Ԫ��
����10�·ݳ����Ĵ�����Ϊm����m����Сֵ��������=���ۼ۩����ϳɱ����̶����ã�
�ڽ���11�·��Ժ�����������ֺ�ת������������VIP�ͻ���10�·�����ۿۼ۵Ļ�����ʵʩ������Żݣ�����ͨ�ͻ���10�·�����ۿۼ۵Ļ�����ʵʩ�۸��ϸ�����֪��VIP�ͻ��Ľ����ʺͶ���ͨ�ͻ����������ȣ����һ��VIP�ͻ���9120Ԫ�������ļ�����һ����ͨ�ͻ���10080Ԫ�������ļ�����ͬ����VIP�ͻ����ܵĽ����ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��һԪ���η�����
��һԪ���η�����![]() .
.
(1)��֤����������ʵ��![]() �����̶���ʵ������
�����̶���ʵ������
(2)��![]() Ϊ��ֵʱ�����̵���������Ϊ�෴������˵������.
Ϊ��ֵʱ�����̵���������Ϊ�෴������˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
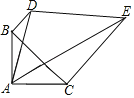
����Ŀ����ͼ����ABC�У�AB��AC����BAC��90�㣬BD��BC��CE��BC����DAE��45�㣬��BD��![]() ��CE��3
��CE��3![]() �����߶�DE��_____��
�����߶�DE��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾��2014�꿪ʼͶ�뼼���Ľ��ʽ𣬾������Ľ������Ʒ�ijɱ����Ͻ��ͣ������������±���
�� �� | 2013 | 2014 | 2015 | 2016 |
Ͷ�뼼���ʽ� | 2.5 | 3 | 4 | 4.5 |
��Ʒ�ɱ� | 7.2 | 6 | 4.5 | 4 |
��1��������������������ݣ���һ�κ����ͷ�����������ȷ����һ�������ܱ�ʾ��仯���ɣ��������ɣ�����������ʽ��
��2���������ֱ仯���ɣ���2017����Ͷ���ʽ�5��Ԫ.
��Ԥ�������ɱ�ÿ����2016�꽵�Ͷ�����Ԫ��
����������2017���ÿ����Ʒ�ɱ����͵�3.2��Ԫ������ҪͶ�뼼���ʽ������Ԫ���������ȷ��0.01��Ԫ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�С��������ķ����������2![]() ��3x��0��
��3x��0��
�ⷨ1���� ԭ���̻�Ϊ2t��3t2��0 �ⷽ��2t��3t2��0����t1��0��t2�� ���� ������ ��x��0�� �����飬x��0�� ���ԣ�ԭ���̵Ľ���x��0�� | �ⷨ2�������2 ��������ͬʱƽ������4x��9x2�� �ⷽ��4x��9x2����x��0�� �����飬x��0�� ���ԣ�ԭ���̵Ľ���x��0�� |
���������ijһ�ַ������������x��![]() ����1�Ľ⣮
����1�Ľ⣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
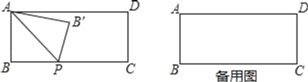
����Ŀ����֪������ABCD��AB��2��BC��5������P�ӵ�B��ʼ���C�˶�������P�ٶ�Ϊÿ��1����λ����APΪ�Գ��ᣬ�ѡ�ABP�۵������á�AB'P�����ABCD�ص��������Ϊy���˶�ʱ��Ϊt�룮
��1�����˶����ڼ���ʱ��B'ǡ������AD�ϣ�
��2����y����t�Ĺ�ϵʽ���Լ�t��ȡֵ��Χ��
��3���ڵڼ���ʱ�ص���������Ǿ���ABCD�����![]() ��
��
��4������PD����PDΪ�Գ��ᣬ����PCD����ԳƱ任���õ���PC'D����tΪ��ֵʱ����P��B'��C'��ͬһֱ���ϣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com