
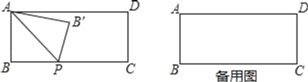
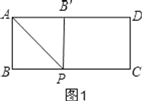
【题目】已知:矩形ABCD,AB=2,BC=5,动点P从点B开始向点C运动,动点P速度为每秒1个单位,以AP为对称轴,把△ABP折叠,所得△AB'P与矩形ABCD重叠部分面积为y,运动时间为t秒.
(1)当运动到第几秒时点B'恰好落在AD上;
(2)求y关于t的关系式,以及t的取值范围;
(3)在第几秒时重叠部分面积是矩形ABCD面积的![]() ;
;
(4)连接PD,以PD为对称轴,将△PCD作轴对称变换,得到△PC'D,当t为何值时,点P、B'、C'在同一直线上?
【答案】(1)当运动到第2秒时点B′恰好落在AD上;(2)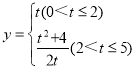 ;(3)第4秒时,重叠部分面积都是矩形ABCD面积的
;(3)第4秒时,重叠部分面积都是矩形ABCD面积的![]() ;(4)当t为1秒或4秒时,点P,B′,C′在同一直线上.
;(4)当t为1秒或4秒时,点P,B′,C′在同一直线上.
【解析】
(1)点B′落在AD上时,四边形ABPB′为正方形,所以t=2;
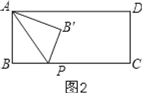
(2)分两种情况讨论:①当0≤t≤2时,如图2,重叠部分面积就是△APB′的面积,即△APB的面积;
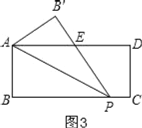
②当2<t≤5时,如图3,重叠部分面积就是△APE的面积,先根据勾股定理表示出AE的长,再利用面积公式求△APE的面积;
(3)分别将①和②中的y等于矩形ABCD面积的![]() ,求出对应的t值即可;
,求出对应的t值即可;
(4)点P,B′,C′在同一直线上时,△AB′P∽△PC′D,得![]() ,列一元二次方程,求出t的值即可.
,列一元二次方程,求出t的值即可.
解:(1)如图1,由折叠得:∠AB′P=∠B=90![]() ,AB=AB′=2,
,AB=AB′=2,
∵四边形ABCD为矩形,
∴∠BAB′=90![]() ,
,
∴四边形ABPB′为正方形,
∴BP=AB=2,
∵动点P速度为每秒1个单位,
∴t=2,
即当运动到第2秒时点B′恰好落在AD上;
(2)分两种情况:①当0≤t≤2时,如图2,PB=t,
由折叠得:S△AB′P=S△ABP,
∴y=S△ABP=![]() ABPB=
ABPB=![]() ×2×t=t,
×2×t=t,
②当2<t≤5时,如图3,
由折叠得:∠APB=∠APE,PB=PB′=t,
∵AD∥BC,
∴∠DAP=∠APB,
∴∠DAP=∠APE,
∴AE=PE,
设AE=x,则PE=x,B′E=t﹣x,
由勾股定理得:22+(t﹣x)2=x2,
x=![]() ,
,
∴![]() ,
,
综上所述: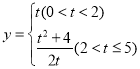 ;
;
(3)①y=t=![]() ×2×5,
×2×5,
∴t=2.5
②![]() =
=![]() ×2×5,
×2×5,
∴t1=1(舍),t2=4,
综上所述:在第4秒时,重叠部分面积都是矩形ABCD面积的![]() ;
;
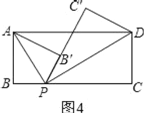
(4)如图4,点P,B′,C′在同一直线上,
由折叠得:∠APB=∠APB′,∠C′PD=∠CPD,
∴∠APC′+∠C′PD=![]() ×180°=90°,
×180°=90°,
∵∠PAB′+∠APB′=90°,
∴∠PAB′=∠C′PD,
∵∠AB′P=∠C′=90°,
∴△AB′P∽△PC′D,
∴![]() ,
,
∴![]() ,
,
解得:t1=1,t2=4,如图5所示,
∴当t为1秒或4秒时,点P,B′,C′在同一直线上.



 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
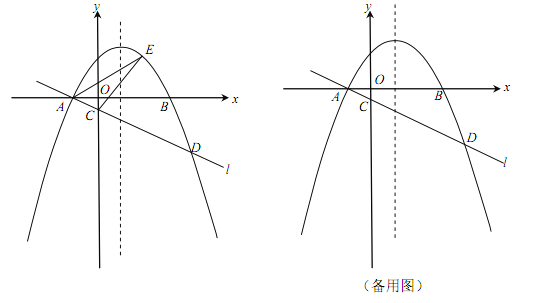
【题目】(本小题满分12分)如图,在平面直角坐标系xOy中,抛物线![]() (
(![]() )与x轴交于A,B两点(点A在点B的左侧),经过点A的直线l:
)与x轴交于A,B两点(点A在点B的左侧),经过点A的直线l:![]() 与y轴负半轴交于点C,与抛物线的另一个交点为D,且CD=4AC.
与y轴负半轴交于点C,与抛物线的另一个交点为D,且CD=4AC.
(1)直接写出点A的坐标,并求直线l的函数表达式(其中k,b用含a的式子表示);
(2)点E是直线l上方的抛物线上的动点,若△ACE的面积的最大值为![]() ,求a的值;
,求a的值;
(3)设P是抛物线的对称轴上的一点,点Q在抛物线上,以点A,D,P,Q为顶点的四边形能否成为矩形?若能,求出点P的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
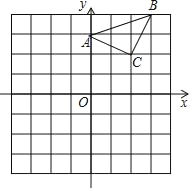
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场销售某种冰箱,该种冰箱每台进价为2500元,已知原销售价为每台2900元时,平均每天能售出8台.若在原销售价的基础上每台降价50元,则平均每天可多售出4台.设每台冰箱的实际售价比原销售价降低了![]() 元.
元.
(1)填表:
每天的销售量/台 | 每台销售利润/元 | |
降价前 | 8 | 400 |
降价后 |
(2)商场为使这种冰箱平均每天的销售利润达到最大时,则每台冰箱的实际售价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面四个实验中,实验结果概率最小的是( )

A.如(1)图,在一次实验中,老师共做了400次掷图钉游戏,并记录了游戏的结果绘制了下面的折线统计图,估计出的钉尖朝上的概率
B.如(2)图,是一个可以自由转动的转盘,任意转动转盘,当转盘停止时,指针落在蓝色区域的概率
C.如(3)图,有一个小球在的地板上自由滚动,地板上的每个格都是边长为1的正方形,则小球在地板上最终停留在黑色区域的概率
D.有7张卡片,分别标有数字1,2,3,4,6,8,9,将它们背面朝上洗匀后,从中随机抽出一张,抽出标有数字“大于6”的卡片的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有四张正面分别印有![]() 和
和![]() 四种图案,并且其余完全相同的卡片,现将印有图案的一面朝下,并打乱摆放顺序,请用列表或画树状图的方法解决下列问题:
四种图案,并且其余完全相同的卡片,现将印有图案的一面朝下,并打乱摆放顺序,请用列表或画树状图的方法解决下列问题:

(1)现从中随机抽取一张,记下图案后放回,再从中随机抽取一张卡片,求两次摸到的卡片上印有图案都是轴对称图形的概率;
(2)现从中随机抽取-张,记下图案后不放回,再从中随机抽取一张卡片,求两次摸到的卡片上印有图案都是中心对称图形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
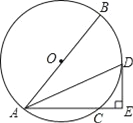
【题目】如图,已知⊙O的直径AB=10,弦AC=6,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E.
(1)求证:DE是⊙O的切线.
(2)求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年5月6日,中国第一条具有自主知识产权的长沙磁浮线正式开通运营,该路线连接了长沙火车南站和黄花国际机场两大交通枢纽,沿线生态绿化带走廊的建设尚在进行中,届时将给乘客带来美的享受.星城渣土运输公司承包了某标段的土方运输任务,拟派出大、小两种型号的渣土运输车运输土方,已知2辆大型渣土运输车与3辆小型渣土运输车一次共运输土方31吨,5辆大型渣土运输车与6辆小型渣土运输车一次共运输土方70吨.
(1)一辆大型渣土运输车和一辆小型渣土运输车一次各运输土方多少吨?
(2)该渣土运输公司决定派出大、小两种型号的渣土运输车共20辆参与运输土方,若每次运输土方总量不少于148吨,且小型渣土运输车至少派出2辆,则有哪几种派车方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com