
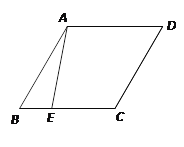
【题目】如图,已知菱形ABCD中,∠B=60°,点E在边BC上,∠BAE=25°,把线段AE绕点A逆时针方向旋转,使点E落在边CD上,那么旋转角![]() 的度数为______.
的度数为______.
【答案】60°或 70°.
【解析】
连接AC,根据菱形的性质及等边三角形的判定易证△ABC是等边三角形.分两种情况:①将△ABE绕点A逆时针旋转60°,点E可落在边DC上,此时△ABE与△ABE1重合;②将线段AE绕点A逆时针旋转70°,点E可落在边DC上,点E与点E2重合,此△AEC≌△AE2C.
连接AC.
∵菱形ABCD中,∠ABC=60°,
∴△ABC是等边三角形,
∴∠BAC=∠ACB=60°,
∴∠ACD=60°.
本题有两种情况:
①如图,将△ABE绕点A逆时针旋转,使点B与点C重合,点E与点E1重合,此时△ABE≌△ABE1,AE=AE1,旋转角α=∠BAC=60°;

②∵∠BAC=60°,∠BAE=25°,
∴∠EAC=35°.
如图,将线段AE绕点A逆时针旋转70°,使点E到点E2的位置,
此时△AEC≌△AE2C,AE=AE2,旋转角α=∠EAE2=70°.

综上可知,符合条件的旋转角α的度数为60度或70度.


科目:初中数学 来源: 题型:
【题目】如图,将一副三角板中含有30°角的三角板的直角顶点落在等腰直角三角形的斜边的中点D处,并绕点D旋转,两直角三角板的两直角边分别交于点E,F,下列结论:①DE=DF;②S四边形AEDF=S△BED+S△CFD;③S△ABC=EF2;④EF2=BE2+CF2,其中正确的序号是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市三景区是人们节假日游玩的热点景区,某学校对九(1)班学生“五一”小长假随父母到这三个景区游玩的计划做了全面调查,调查分四个类别,A:三个景区;B:游两个景区;C:游一个景区;D:不到这三个景区游玩,现根据调查结果绘制了不完全的条形统计图和扇形统计图如下:
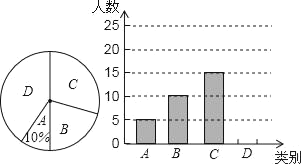
请结合图中信息解答下列问题:
(1)九(1)班现有学生 人,在扇形统计图中表示“B类别”的扇形的圆心角的度数为 ;
(2)请将条形统计图补充完整;
(3)若该校九年级有1000名学生,求计划“五一”小长假随父母到这三个景区游玩的学生多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
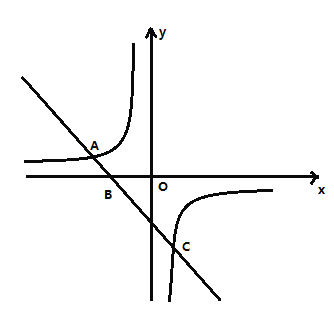
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]()
![]() 的图象交于点
的图象交于点![]() 两点,其中点
两点,其中点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
![]() 求一次函数和反比例函数的表达式;
求一次函数和反比例函数的表达式;
![]() 求
求![]() 点坐标;
点坐标;
![]() 根据图象,直接写出不等式
根据图象,直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2015德阳)大华服装厂生产一件秋冬季外套需面料1.2米,里料0.8米,已知面料的单价比里料的单价的2倍还多10元,一件外套的布料成本为76元.
(1)求面料和里料的单价;
(2)该款外套9月份投放市场的批发价为150元/件,出现购销两旺态势,10月份进入批发淡季,厂方决定采取打折促销.已知生产一件外套需人工等固定费用14元,为确保每件外套的利润不低于30元.
①设10月份厂方的打折数为m,求m的最小值;(利润=销售价﹣布料成本﹣固定费用)
②进入11月份以后,销售情况出现好转,厂方决定对VIP客户在10月份最低折扣价的基础上实施更大的优惠,对普通客户在10月份最低折扣价的基础上实施价格上浮.已知对VIP客户的降价率和对普通客户的提价率相等,结果一个VIP客户用9120元批发外套的件数和一个普通客户用10080元批发外套的件数相同,求VIP客户享受的降价率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】天水某公交公司将淘汰某一条线路上“冒黑烟”较严重的公交车,计划购买A型和B型两行环保节能公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元,
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在该条线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1220万元,且确保这10辆公交车在该线路的年均载客量总和不少于650万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少总费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() 的图象经过点
的图象经过点![]() ,直线
,直线![]() 与双曲线交于另一点
与双曲线交于另一点![]() ,作
,作![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,连接
,连接![]() .
.
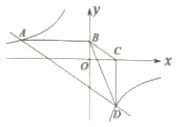
(1)求![]() 的值;
的值;
(2)若![]() ,求直线
,求直线![]() 的解析式;
的解析式;
(3)若![]() ,其它条件不变,直接写出
,其它条件不变,直接写出![]() 与
与![]() 的位置关系.
的位置关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
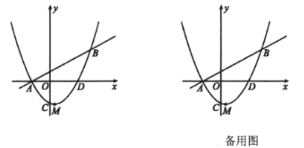
【题目】如图,已知直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() ,
,![]() 两点,抛物线
两点,抛物线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴正半轴于
轴正半轴于![]() 点,抛物线的顶点为
点,抛物线的顶点为![]() .
.
(1)求抛物线的解析式;
(2)设点![]() 为直线
为直线![]() 下方的抛物线上一动点,当
下方的抛物线上一动点,当![]() 的面积最大时,求
的面积最大时,求![]() 的面积及点
的面积及点![]() 的坐标;
的坐标;
(3)若点![]() 为
为![]() 轴上一动点,点
轴上一动点,点![]() 在抛物线上且位于其对称轴右侧,当
在抛物线上且位于其对称轴右侧,当![]() 与
与![]() 相似时,求
相似时,求![]() 点的坐标.
点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com