

分析 (1)过A作AP⊥GF于点P,如图,利用矩形的性质得AP=BF=CF+BC=12,AB=PF=1.4,再在Rt△PAG中,根据正切的定义可计算出GP=AP•tan37°=9(米),于是得到GF=GP+PF≈10.4(米);
(2)在直角△MNF中,利用勾股定理计算出NF=4,然后通过比较梯子、竹竿和身高的和与挂在树上的风筝的高度的大小进行判断.
解答 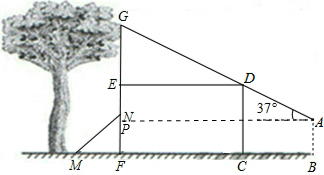 解:(1)过A作AP⊥GF于点P,如图,则AP=BF=CF+BC=7+5=12,AB=PF=1.4,∠GAP=37°,
解:(1)过A作AP⊥GF于点P,如图,则AP=BF=CF+BC=7+5=12,AB=PF=1.4,∠GAP=37°,
在Rt△PAG中,tan∠PAG=$\frac{GP}{AP}$,
∴GP=AP•tan37°≈12×0.75=9(米),
∴GF=GP+PF=9+1.4≈10.4(米);
(2)由题意可知MN=5,MF=3,
在直角△MNF中,NF=$\sqrt{M{N}^{2}-M{F}^{2}}$=4,
∵4+1.65+5=10.65,
10.65>10.4,
即梯子、竹竿和身高的和大于挂在树上的风筝的高度,
∴兵兵充分利用梯子和一根5米长的竹竿能触到挂在树上的风筝.
点评 本题考查了解直角三角形的应用:将实际问题抽象为数学问题(画出平面图形,构造出直角三角形转化为解直角三角形问题),根据题目已知特点选用适当锐角三角函数或边角关系去解直角三角形,得到数学问题的答案,再转化得到实际问题的答案.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:解答题
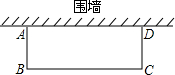 如图,利用已有的围墙对邻边不等的矩形花圃ABCD修建栅栏,已知三边所围的栅栏的总长度是6m,且可利用的围墙长度超过6m,若矩形ABCD的面积为4m2,试求边AB的长度.
如图,利用已有的围墙对邻边不等的矩形花圃ABCD修建栅栏,已知三边所围的栅栏的总长度是6m,且可利用的围墙长度超过6m,若矩形ABCD的面积为4m2,试求边AB的长度.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 甲、乙两人同时从A地出发到B地去,已知甲骑自行车,乙步行,甲到达B地后用半小时办完事后按原速返回.甲、乙两人之间的距离y(单位:千米)与行驶时间t(单位:时)之间的函数关系如图所示,则图中a的值是$\frac{25}{14}$.
甲、乙两人同时从A地出发到B地去,已知甲骑自行车,乙步行,甲到达B地后用半小时办完事后按原速返回.甲、乙两人之间的距离y(单位:千米)与行驶时间t(单位:时)之间的函数关系如图所示,则图中a的值是$\frac{25}{14}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
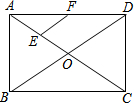 如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=5cm,BC=12cm,则EF=$\frac{13}{4}$ cm.
如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=5cm,BC=12cm,则EF=$\frac{13}{4}$ cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com