
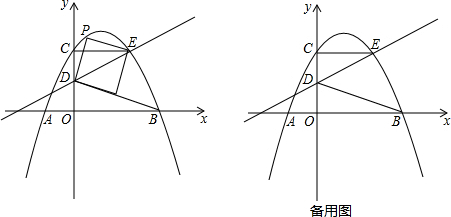
分析 (1)先确定出点E的纵坐标,进而利用一次函数解析式得出点E的坐标,然后结合点C、E的坐标,利用待定系数法可求得抛物线的解析式;
(2)先证明△QEF∽△DEC进而用t表示EF,并用勾股定理求出DE,进而用t表示DF,然后求出B点坐标,并求出BD的长,过B作BN⊥DE于N,设直线DE与x轴交于点M,利用△BDM的面积求出BN的长,再利用∠NDB的正弦函数求出其度数,可得到△FDH为等腰直角三角形,最后利用三角形的面积公式列式化简即可;
(3)首先判断出点D、M、E、P在以MP为直径的圆上,进而利用圆周角定理可知∠PDM=90°,∠PCE=∠PME=45°,则有CG=PG,据此求出点P的坐标,然后利用勾股定理的逆定理得到∠DPE=90°,可判断四边形PDME是矩形,进而判断四边形PMBE是平行四边形,再利用平行四边形的面积求法列式计算即可.
解答 解:(1)∵CE⊥y轴,C(0,4),且E在直线y=$\frac{1}{2}$x+2上,
∴E点的纵坐标为4,
由$\frac{1}{2}$x+2=4,得x=4,
∴E(4,4),
把C、E两点坐标代入抛物线解析式得$\left\{\begin{array}{l}{c=4}\\{-\frac{16}{3}+4b+c=4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=\frac{4}{3}}\\{c=4}\end{array}\right.$,
∴抛物线的解析式为y=-$\frac{1}{3}$x2+$\frac{4}{3}$x+4;
(2)由直线y=$\frac{1}{2}$x+2与y轴交于点D,得D(0,2),
如图1,由题意可知CQ=t,QE=4-t,DC=2,则DE=$\sqrt{D{C}^{2}+C{E}^{2}}$=$2\sqrt{5}$,
∵∠QEF=∠DEC,∠QFE=∠DCE=90°,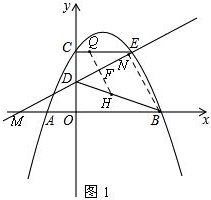
∴△QEF∽△DEC,
∴QE:DE=EF:EC,即(4-t):$2\sqrt{5}$=EF:4,
解得EF=$-\frac{2\sqrt{5}}{5}t+\frac{8\sqrt{5}}{5}$,
∴DF=DE-EF=$\frac{2\sqrt{5}}{5}t+\frac{2\sqrt{5}}{5}$,
抛物线y=-$\frac{1}{3}$x2+$\frac{4}{3}$x+4,令y=0,得-$\frac{1}{3}$x2+$\frac{4}{3}$x+4=0,
解得x1=-2,x2=6,
∴B(6,0),
∴BD=$\sqrt{O{D}^{2}+O{B}^{2}}$=$2\sqrt{10}$,
过B作BN⊥DE于N,设直线DE与x轴交于点M,则M(-4,0),DM=$\sqrt{O{F}^{2}+O{D}^{2}}$=$2\sqrt{5}$,
∴S△BDM=$\frac{1}{2}$DM•BN=$\frac{1}{2}$BM•OD,
∴BN=$\frac{BF•OD}{DM}$=$2\sqrt{5}$,
∴sin∠NDB=$\frac{BN}{BD}$=$\frac{\sqrt{2}}{2}$,
∴∠NDB=45°,
∴△FDH是等腰直角三角形,DF=FH=$\frac{2\sqrt{5}}{5}t+\frac{2\sqrt{5}}{5}$,
∴S=$\frac{1}{2}$DF•FH=$\frac{1}{2}(\frac{2\sqrt{5}}{5}t+\frac{2\sqrt{5}}{5})^{2}$=$\frac{2}{5}$t2+$\frac{4}{5}$t+$\frac{2}{5}$,
即S=$\frac{2}{5}$t2+$\frac{4}{5}$t+$\frac{2}{5}$(0≤t≤4);
(3)如图2,过P作PG⊥CE于G,设P(m,-$\frac{1}{3}$m2+$\frac{4}{3}$m+4),连接PC、PD,
∵△PEM是等腰直角三角形,PE=EM,
∴∠EPM=∠EMP=45°,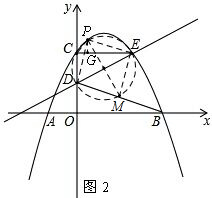
又∵∠EDM=45°,
∴点D、M、E、P在以MP为直径的圆上,
∴∠PDM=90°,∠PCE=∠PME=45°(圆周角定理),
∴CG=PG,
∵PG=-$\frac{1}{3}$m2+$\frac{4}{3}$m+4-4=-$\frac{1}{3}$m2+$\frac{4}{3}$m,
∴-$\frac{1}{3}$m2+$\frac{4}{3}$m=m,
∴m=1或m=0(不合题意,舍去),
∴P(1,5),
∴PG=CG=1,GE=3,PE=$\sqrt{P{G}^{2}+G{E}^{2}}$=$\sqrt{10}$,ME=$\sqrt{10}$,
∴DP=$\sqrt{{1}^{2}+(5-2)^{2}}$=$\sqrt{10}$,
∴DP2+PE2=DE2,
∴∠DPE=90°,
又∵∠PDM=90°,∠PEM=90°,
∴四边形PDME是矩形,
∴PE∥BD,PE=DM=$\sqrt{10}$,
∴BM=BD-DM=$\sqrt{10}$,
∴BM=PE,
∴四边形PMBE是平行四边形,
∴四边形PMBE的面积为PE•ME=$\sqrt{10}$•$\sqrt{10}$=10.
点评 本题考查了二次函数的综合应用,勾股定理及其逆定理的应用,平行四边形和矩形的判定与性质,圆周角定理,相似三角形的判定与性质等知识,涉及的知识较多,综合性较强,具有一定的难度,解答本题时要注意数形结合思想与方程思想的运用.


科目:初中数学 来源: 题型:解答题
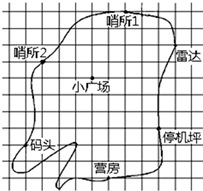 南海诸岛自古以来就是中华民族神圣领土的一部分,我国对南海诸岛及其附近海域拥有无可争辩的主权.如图是我国南沙群岛中某个小岛的平面示意图,小明建立了平面直角坐标系后,营房的坐标为(2,-5),哨所2的坐标为(-2,2).
南海诸岛自古以来就是中华民族神圣领土的一部分,我国对南海诸岛及其附近海域拥有无可争辩的主权.如图是我国南沙群岛中某个小岛的平面示意图,小明建立了平面直角坐标系后,营房的坐标为(2,-5),哨所2的坐标为(-2,2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1>y2 | B. | y1<y2 | ||
| C. | y1=y2 | D. | y1与y2的大小不一定 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
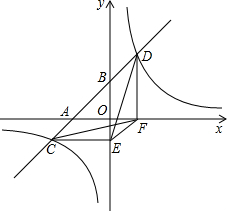 如图,一次函数y=ax+b的图象与x轴,y轴交于A,B两点,与反比例函数y=$\frac{k}{x}$的图象相交于C,D两点,分别过C,D两点作y轴,x轴的垂线,垂足为E,F,连接CF,DE.有下列四个结论:
如图,一次函数y=ax+b的图象与x轴,y轴交于A,B两点,与反比例函数y=$\frac{k}{x}$的图象相交于C,D两点,分别过C,D两点作y轴,x轴的垂线,垂足为E,F,连接CF,DE.有下列四个结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
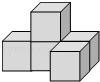 如图所示的几何体是由5个相同的小正方体组成的,下列有关三视图面积的说法中正确的是( )
如图所示的几何体是由5个相同的小正方体组成的,下列有关三视图面积的说法中正确的是( )| A. | 左视图面积最大 | B. | 俯视图面积最小 | ||
| C. | 左视图与主视图面积相等 | D. | 俯视图与主视图面积相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
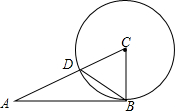 已知△ABC,以顶点C为圆心、CB为半径作圆交AC于点D,连接DB.若∠ACB=2∠ABD,
已知△ABC,以顶点C为圆心、CB为半径作圆交AC于点D,连接DB.若∠ACB=2∠ABD,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com