
【题目】某通讯公司推出了移动电话的两种计费方式(详情见下表)。
月使用费/元 | 主叫限定时间/分 | 主叫超时费/(元/分) | 被叫 | |
方式一 | 58 | 150 | 0.25 | 免费 |
方式二 | 88 | 350 | 0.19 | 免费 |

设一个月内使用移动电话主叫的时间为![]() 分(
分(![]() 为正整数),请根据表中提供的信息回答下列问题:
为正整数),请根据表中提供的信息回答下列问题:
(1)用含有![]() 的式子填写下表:
的式子填写下表:
| 150< |
|
| |
方式一计费/元 | 58 |
| 108 |
|
方式二计费/元 | 88 | 88 | 88 |
|
(Ⅰ)当![]() 为何值时,两种计费方式的费用相等?
为何值时,两种计费方式的费用相等?
(Ⅱ)请根据(Ⅰ)和(Ⅱ)的计算及生活经验,直接写出不同时间段,选用哪种计费方式省钱.
【答案】(1)0.25t+20.5;0.25t+20.5;0.19t+21.5;(Ⅰ)270;(Ⅱ)当t<270时,方式一收费更划算;当t=270时方式一收费和方式二收费一样;当t>270时,方式二收费更划算.
【解析】
(1)根据上表及范围即可得出方式一及方式二的收费情况;
(Ⅰ)根据两种方式的收费标准进行计算即可,先判断出两种方式相等时t的大致范围,继而建立方程即可得出答案.
(II)计算出两种方式在各个取值范围的收费情况,然后比较即可得出答案.
(1)①当150<t<350时,方式一收费:58+0.25(t150)=0.25t+20.5;
②当t>350时,方式一收费:108+0.25(t350)=0.25t+20.5;
③方式二当t>350时收费:88+0.19(t350)=0.19t+21.5.
(Ⅰ)∵(0.25t+20.5)(0.19t+21.5)=0.06t1>0,
∴当两种计费方式的费用相等时,t的值在150<t<350取得.
∴列方程0.25t+20.5=88,
解得t=270.
即当主叫时间为270分时,两种计费方式的费用相等。
(Ⅱ)当![]() 时,方式一收费-方式二收费y=58-88=-30<0,即可得方式一收费更划算;
时,方式一收费-方式二收费y=58-88=-30<0,即可得方式一收费更划算;
当![]() 时,方式一收费-方式二收费y=0.25t+20.5-88<0, 即可得方式一收费更划算;
时,方式一收费-方式二收费y=0.25t+20.5-88<0, 即可得方式一收费更划算;
当t=270时,方式一收费-方式二收费y0.25t+20.5-88=0,即方式一收费和方式二收费一样;
当![]() 时,方式一收费-方式二收费y=0.25t+20.5-88>0,即可得方式二收费更划算;
时,方式一收费-方式二收费y=0.25t+20.5-88>0,即可得方式二收费更划算;
当t=350时,方式一收费-方式二收费y=108-88=20>0,即可得方式二收费更划算;
当t>350时,方式一收费-方式二收费y=0.25t+20.5-(0.19t+21.5)=0.06t-1>0, 即可得方式二收费更划算.
综上可知,当t<270时,方式一收费更划算;当t=270时方式一收费和方式二收费一样;当t>270时,方式二收费更划算.


科目:初中数学 来源: 题型:
【题目】嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图1的四边形ABCD,并写出了如下不完整的已知和求证.
已知:如图1,在四边形ABCD中,BC=AD,AB=

求证:四边形ABCD是 四边形.
(1)在方框中填空,以补全已知和求证;
(2)按嘉淇同学的思路写出证明过程;
(3)用文字叙述所证命题的逆命题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点O为直线AB上一点,将一个直角三角板COD的直角顶点放在点O处,并使OC边始终在直线AB的上方,OE平分∠BOC.

(1)如图1,若∠DOE=70°,则∠AOC =___________°;
(2)如图1,若∠DOE=α,求∠AOC的度数;(用含α的式子表示)
(3)如图2,在(2)的条件下,若在∠AOC的内部有一条射线OF,满足∠BOE =![]() (∠AOF-∠DOE),试确定∠AOF与∠DOE之间的数量关系,并说明理由.
(∠AOF-∠DOE),试确定∠AOF与∠DOE之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用火柴棒按如图方式拼图,第1个图形共用3根火柴棒,第2个图形共用9根火柴棒,第3个图形共用18根火柴棒,……按照这样的方式继续拼图,第n个图形共用_____根火柴棒.(用含n的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
阅读材料:
数轴是学习有理数的一种重要工具,任何有理数都可以用数轴上的点表示,这样能够运用数形结合的方法解决一些问题.例如,两个有理数在数轴上对应的点之间的距离可以用这两个数的差的绝对值表示;
在数轴上,有理数3与1对应的两点之间的距离为|3﹣1|=2;
在数轴上,有理数5与﹣2对应的两点之间的距离为|5﹣(﹣2)|=7;
在数轴上,有理数﹣2与3对应的两点之间的距离为|﹣2﹣3|=5;
在数轴上,有理数﹣8与﹣5对应的两点之间的距离为|﹣8﹣(﹣5)|=3;……
如图1,在数轴上有理数a对应的点为点A,有理数b对应的点为点B,A,B两点之间的距离表示为|a﹣b|或|b﹣a|,记为|AB|=|a﹣b|=|b﹣a|.

解决问题:
(1)数轴上有理数﹣10与﹣5对应的两点之间的距离等于 ;数轴上有理数x与﹣5对应的两点之间的距离用含x的式子表示为 ;若数轴上有理数x与﹣1对应的两点A,B之间的距离|AB|=2,则x等于 ;
联系拓广:
(2)如图2,点M,N,P是数轴上的三点,点M表示的数为4,点N表示的数为﹣2,动点P表示的数为x.
请从A,B两题中任选一题作答,我选择 题.
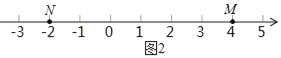
A.①若点P在点M,N两点之间,则|PM|+|PN|= ;
②若|PM|=2|PN|,即点P到点M的距离等于点P到点N的距离的2倍,则x等于 .
B.①若点P在点M,N之间,则|x+2|+|x﹣4|= ;
若|x+2|+|x﹣4|═10,则x= ;
②根据阅读材料及上述各题的解答方法,|x+2|+|x|+|x﹣2|+|x﹣4|的最小值等于 .
查看答案和解析>>
科目:初中数学 来源: 题型:
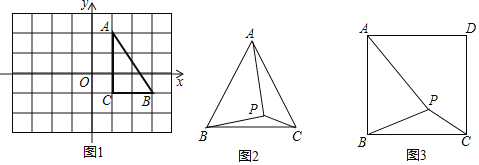
【题目】(1)如图1,在边长为1个单位长度的小正方形组成的网格中,△ABC的三个顶点均在格点上.请按要求画图:将△ABC绕点A按顺时针方向旋转90°,点B的对应点为B′,点C的对应点为C′,连接BB′,则∠AB′B= ;
(2)如图2,在等边三角形ABC内有一点P,且PA=![]() ,PB=2,PC=
,PB=2,PC=![]() ,求∠BPC的度数和等边三角形ABC的边长;
,求∠BPC的度数和等边三角形ABC的边长;
(3)如图3,在正方形ABCD内有一点P,且PA=![]() ,PB=2,PC=
,PB=2,PC=![]() ,求∠BPC的度数和正方形ABCD的边长.
,求∠BPC的度数和正方形ABCD的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着通讯技术迅猛发展,人与人之间的沟通方式更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次统计共抽查了________名学生;
(2)将条形统计图补充完整;
(3)若某校有1000名学生,试估计最喜欢用“微信”沟通的人数;
(4)某天甲、乙两名同学都想从“微信”、“QQ”、“电话”三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选中同一种沟通方式的概率。


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级学生全部参加“初二生物地理会考”,从中抽取了部分学生的生物考试成绩,将他们的成绩进行统计后分为A,B,C,D四等,并将统计结果绘制成如下的统计图,请结合图中所给的信息解答下列问题(说明:测试总人数的前30%考生为A等级,前30%至前70%为B等级,前70%至前90%为C等级,90%以后为D等级)

(1)抽取了 名学生成绩;
(2)请把频数分布直方图补充完整;
(3)扇形统计图中A等级所在的扇形的圆心角度数是 ;
(4)若测试总人数前90%为合格,该校初二年级有900名学生,求全年级生物合格的学生共约多少人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com