
【题目】已知点O为直线AB上一点,将一个直角三角板COD的直角顶点放在点O处,并使OC边始终在直线AB的上方,OE平分∠BOC.

(1)如图1,若∠DOE=70°,则∠AOC =___________°;
(2)如图1,若∠DOE=α,求∠AOC的度数;(用含α的式子表示)
(3)如图2,在(2)的条件下,若在∠AOC的内部有一条射线OF,满足∠BOE =![]() (∠AOF-∠DOE),试确定∠AOF与∠DOE之间的数量关系,并说明理由.
(∠AOF-∠DOE),试确定∠AOF与∠DOE之间的数量关系,并说明理由.
【答案】(1)140°;(2)![]() ;(3)∠AOF+∠DOE=180° (或 ∠AOF与∠DOE互补 ),理由见解析
;(3)∠AOF+∠DOE=180° (或 ∠AOF与∠DOE互补 ),理由见解析
【解析】
(1)由角平分线的性质及同角的余角相等,可得答案;
(2)类比(1),由角平分线的性质及同角的余角相等,可得出∠AOC的度数;
(3)由∠BOE=![]() (∠AOF-∠DOE),得出180°-∠AOC=∠AOF-∠DOE,再根据∠DOE =
(∠AOF-∠DOE),得出180°-∠AOC=∠AOF-∠DOE,再根据∠DOE =![]() ,∠AOC =2
,∠AOC =2![]() 解答即可.
解答即可.
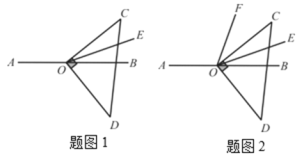
(1)解: ∵∠DOC=90°, ∠DOE=70°,
∴∠COE=20°,
∵OE平分∠BOC,
∴∠COE=∠BOE=20°,
∴∠BOC=40°,
∵∠AOC+∠BOC=180°,
∴∠AOC=140°
(2)解:∵∠DOE =![]()
![]() ∠COE=90°
∠COE=90°![]()
∵OE平分∠BOC
![]() ∠BOC=2∠COE=180°
∠BOC=2∠COE=180°![]()
![]() ∠AOC=180°-∠BOC=180°-(180°
∠AOC=180°-∠BOC=180°-(180°![]() )=
)=![]()
(3)∠AOF+∠DOE=180° (或 ∠AOF与∠DOE互补 )
理由如下:
∵∠BOE=![]() (∠AOF-∠DOE)
(∠AOF-∠DOE)
![]() 2∠BOE= ∠AOF-∠DOE
2∠BOE= ∠AOF-∠DOE
![]() ∠BOC=∠AOF-∠DOE
∠BOC=∠AOF-∠DOE
![]() 180°-∠AOC=∠AOF-∠DOE
180°-∠AOC=∠AOF-∠DOE
∵∠DOE =![]() ,∠AOC =2
,∠AOC =2![]()
![]() ∠AOC=2∠DOE
∠AOC=2∠DOE
![]() 180°-2∠DOE=∠AOF-∠DOE
180°-2∠DOE=∠AOF-∠DOE
![]() ∠AOF+∠DOE=180°,即∠AOF与∠DOE互补.
∠AOF+∠DOE=180°,即∠AOF与∠DOE互补.


 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+2交y轴于A点,交x轴于C点,以O,A,C为顶点作矩形OABC,将矩形OABC绕O点顺时针旋转90°,得到矩形ODEF,直线AC交直线DF于G点.
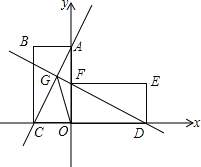
(1)求直线DF的解析式;
(2)求证:GO平分∠CGD;
(3)在角平分线GO上找一点M,使以点G、M、D为顶点的三角形是等腰直角三角形,求出M点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数![]() ,
,![]() 表示的点在数轴上的位置如图所示.
表示的点在数轴上的位置如图所示.
![]()
(1)在数轴上表示出![]() ,
,![]() 的相反数的位置;
的相反数的位置;
(2)若数![]() 与其相反数相距20个单位长度,则
与其相反数相距20个单位长度,则![]() 表示的数是多少?
表示的数是多少?
(3)在(2)的条件下,若数![]() 表示的点与数
表示的点与数![]() 的相反数表示的点相距5个单位长度,求
的相反数表示的点相距5个单位长度,求![]() 表示的数是多少?
表示的数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E为矩形ABCD外一点,AE=DE,连接EB、EC分别与AD相交于点F、G.求证: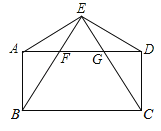
(1)△EAB≌△EDC;
(2)∠EFG=∠EGF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠BAC的平分线与BC的垂直平分线DG相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,AB=6,AC=3,则BE=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG.
(1)求证:△ABG≌△AFG;(2)求BG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通讯公司推出了移动电话的两种计费方式(详情见下表)。
月使用费/元 | 主叫限定时间/分 | 主叫超时费/(元/分) | 被叫 | |
方式一 | 58 | 150 | 0.25 | 免费 |
方式二 | 88 | 350 | 0.19 | 免费 |

设一个月内使用移动电话主叫的时间为![]() 分(
分(![]() 为正整数),请根据表中提供的信息回答下列问题:
为正整数),请根据表中提供的信息回答下列问题:
(1)用含有![]() 的式子填写下表:
的式子填写下表:
| 150< |
|
| |
方式一计费/元 | 58 |
| 108 |
|
方式二计费/元 | 88 | 88 | 88 |
|
(Ⅰ)当![]() 为何值时,两种计费方式的费用相等?
为何值时,两种计费方式的费用相等?
(Ⅱ)请根据(Ⅰ)和(Ⅱ)的计算及生活经验,直接写出不同时间段,选用哪种计费方式省钱.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BF为⊙O的直径,直线AC交⊙O于A,B两点,点D在⊙O上,BD平分∠OBC,DE⊥AC于点E.
(1)求证:直线DE是⊙O的切线;
(2)若 BF=10,sin∠BDE=![]() ,求DE的长.
,求DE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com