
如图,已知点E在△ABC的边AB上,∠C=90°,∠BAC的平分线交BC于点D,且D在以AE为直径的⊙O上.
(1)求证:BC是⊙O的切线;
(2)已知∠B=30°,CD=4,求线段AB的长.


【考点】切线的判定;勾股定理.
【专题】证明题.
【分析】(1)连结OD,根据角平分线的定义得到∠BAD=∠CAD,而∠OAD=∠ODA,则∠ODA=∠CAD,于是判断OD∥AC,由于∠C=90°,所以∠ODB=90°,然后根据切线的判定定理即可得到结论;
(2)由∠B=30°得到∠BAC=60°,则∠CAD=30°,在Rt△ADC中,根据含30度的直角三角形三边的关系得到AC=4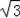
 ,然后在Rt△ABC中,根据含30度的直角三角形三边的关系可得到AB=8
,然后在Rt△ABC中,根据含30度的直角三角形三边的关系可得到AB=8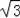
 .
.
【解答】(1)证明:连结OD,如图,
∵∠BAC的平分线交BC于点D,
∴∠BAD=∠CAD,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠ODA=∠CAD,
∴OD∥AC,
∵∠C=90°,
∴∠ODB=90°,
∴OD⊥BC,
∴BC是⊙O的切线;
(2)解:∵∠B=30°,
∴∠BAC=60°,
∴∠CAD=30°,
在Rt△ADC中,DC=4,
∴AC=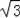
 DC=4
DC=4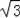
 ,
,
在Rt△ABC中,∠B=30°,
∴AB=2AC=8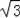
 .
.

【点评】本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了含30度的直角三角形三边的关系.


科目:初中数学 来源: 题型:
如图,点A和点D都在线段BC的垂直平分线上.连接AB,AC,DB,DC.如果∠1=20°,∠2=50°.那么∠BAC比∠BDC( )
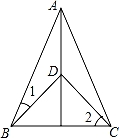
A.大40° B.小40° C.大30° D.小30°
查看答案和解析>>
科目:初中数学 来源: 题型:
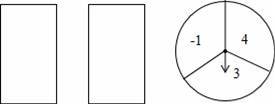
小云玩抽卡片和旋转盘游戏,有两张正面分别标有数字1,2的不透明卡片,背面完全相同;转盘被平均分成3个相等的扇形,并分别标有数字﹣1,3,4(如图所示),小云把卡片背面朝上洗匀后从中随机抽出一张,记下卡片上的数字;然后转动转盘,转盘停止后,记下指针所在区域的数字(若指针在分格线上,则重转一次,直到指针指向某一区域为止).
(1)请用列表或树状图的方法(只选其中一种),表示出两次所得数字可能出现的所有结果;
(2)求出两个数字之积为负数的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
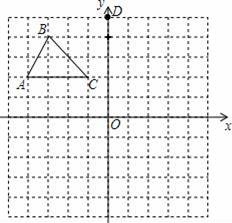
如图所示的网格图中,每小格都是边长为1的正方形,△ABC的三个顶点都在格点上,在建立直角坐标系后,点C的坐标(﹣1,2).
(1)画出△ABC绕点D(0,5)逆时针旋转90°后的△A1B1C1;并标出A1,B1,C1的坐标.
(2)画出△ABC关于原点O的中心对称图形△A2B2C2,并标出A2,B2,C2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
为了市民出行更加方便,天津市政府大力发展公共交通,2013年天津市公共交通客运量约为1608000000人次,将1608000000用科学记数法表示为( )
A.160.8×107 B.16.08×108 C.1.608×109 D.0.1608×1010
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com