Question

11．如图1，在梯形ABCD中，AD∥BC，∠C=90°，点E从点B出发，以某一速度沿折线BA-AD-DC向点C匀速运动；点F从点C出发，以每秒1个单位长的速度向点B匀速运动，点E、F同时出发同时停止．设运动时间为t秒时，△BEF的面积为y，已知y与t的函数关系如图2所示．请根据图中的信息，解答下列问题：
（1）点E运动到A、D两点时，y的值分别是7和4；
（2）求BC和CD的长；
（3）求点E的运动速度；
（4）当t为何值时，△BEF与梯形ABCD的面积之比为1：3？

Answer 1

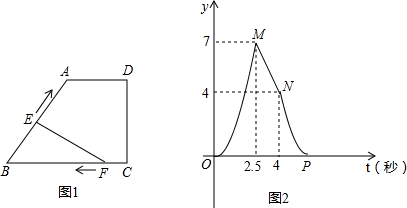
分析 （1）根据图2可以得到OM表示E在BA段，MN表示E在AD段，NP表示E在DC段，据此即可判断；
（2）根据E在A点和D点时，△EBF的面积分别是7和4，利用面积公式即可得到关于CD和BC的方程组，即可求得BC和CD的长；
（3）根据两个点的运动时间以及（2）中求得的运动距离，即可求得运动的速度；
（4）首先求得梯形ABCD的面积，当E在AB上时，过点E作EH⊥BC于点H，△EBH∽△ABG，根据相似三角形的对应边的比相等，即可得到关于时间的方程，从而求解．

解答 解：（1）点E运动到A、D两点时，在图2中对应的点是M，N两点，则对应的值是：7和4；
故答案为：7，4；

（2）当t=2.5秒时，△EBF的面积为y=$\frac{1}{2}$•（BC-CF）•CD=7，
即：$\frac{1}{2}$（BC-$\frac{5}{2}$）•CD=7，
当t=4秒时，△EBF的面积为y=$\frac{1}{2}$•（BC-CF）•CD=4，
即：$\frac{1}{2}$（BC-4）•CD=4．
∴CD=4，BC=6；

（3）∵BC=6，点F的速度是每秒1个单位，
∴BC=6，
∴点E从D运动到C用时为6-4=2秒，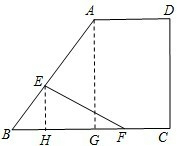
又∵CD=4，
∴点E的运动速度为每秒2个单位；

（4）∵k=2，
∴AD=3，AB=5，
∴S_△EBF=6，S_梯形ABCD=18，
由题意可知运动过程中有两个时刻△EBF的面积等于6，
①当E在AB上时，过点E作EH⊥BC于点H，过A作AG⊥BC于G，
∴EH∥AG，
∴△EBH∽△ABG，
∴$\frac{BE}{AB}=\frac{EH}{AG}$，
∴EH=$\frac{8}{5}$t，
∴$\frac{1}{2}$×$\frac{8}{5}$t×（6-t）=6，解得t=$\frac{6±\sqrt{6}}{2}$，
∵t≤2.5．
∴t=$\frac{6-\sqrt{6}}{2}$
②当E在AD上时，$\frac{1}{2}$×4×（6-t）=6，解得t=3．
综上所述，当t=$\frac{6-\sqrt{6}}{2}$或t=3秒时，△EBF与梯形ABCD的面积之比为1：3．

点评 本题考查了相似三角形的判定与性质，三角形的面积的计算，正确的识别图形，正确利用题目中的图形的关系，转化成方程问题求解是关键．