
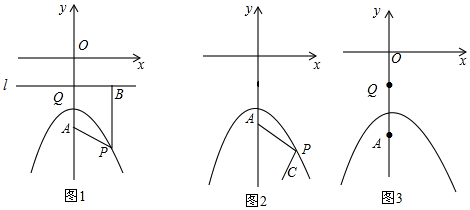
分析 (1)利用二次函数图象上点的坐标特征,设P(m,-$\frac{1}{4}$m2-2),则B(m,-1),然后根据两点间的距离公式计算出PA和PB,从而可判断它们相等;
(2)①过点Q作QB∥x轴,过P点作PB⊥QB于B点,如图2,由(1)得PB=PA,根据两点之间线段最短,当点P、B、C共线时,此时P点的横坐标为2,然后计算对应的函数值即可得到P点坐标;
②过点Q(0,-1)作直线l平行于x轴,作PB⊥l于B,DE⊥l于E,如图3,由(1)得PB=PA,DE=DA,再证明△QDE∽△QPB,利用相似比得到$\frac{QE}{QB}$=$\frac{DE}{PB}$=$\frac{1}{4}$,设P(m,-$\frac{1}{4}$m2-2),则B(m,-1),PB=$\frac{1}{4}$m2+1,易得E点坐标为($\frac{1}{4}$m,-1),D点坐标为[$\frac{1}{4}$m,-$\frac{1}{4}$($\frac{1}{4}$m)2-2],则ED=$\frac{1}{64}$m2+1,然后根据DE和PB的数量关系列方程$\frac{1}{4}$m2+1=4($\frac{1}{64}$m2+1),解方程求出m,从而得到P点坐标,最后利用待定系数法求直线PQ的解析式.
解答 解:(1)PA与PB相等.
理由如下:设P(m,-$\frac{1}{4}$m2-2),则B(m,-1),
∵PA=$\sqrt{{m}^{2}+(-\frac{1}{4}{m}^{2}-2+3)^{2}}$=$\sqrt{(\frac{1}{4}{m}^{2}+1)^{2}}$=$\frac{1}{4}$m2+1,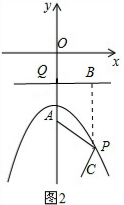
PB=-1-(-$\frac{1}{4}$m2-2)=$\frac{1}{4}$m2+1,
∴PA=PB.
故答案为=;
(2)①存在.
过点Q作QB∥x轴,过P点作PB⊥QB于B点,如图2,由(1)得PB=PA,则PA+PC=PB+PC,
当点P、B、C共线时,PB+PC最小,此时PC⊥QB,P点的横坐标为2,
当x=2时,y=-$\frac{1}{4}$x2-2=-$\frac{1}{4}$×4-2=-3,
即此时P点坐标为(2,-3);
②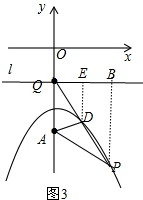 过点Q(0,-1)作直线l平行于x轴,作PB⊥l于B,DE⊥l于E,如图3,由(1)得PB=PA,DE=DA,
过点Q(0,-1)作直线l平行于x轴,作PB⊥l于B,DE⊥l于E,如图3,由(1)得PB=PA,DE=DA,
∵PA=4AD,
∴PB=4DE,
∵DE∥PB,
∴△QDE∽△QPB,
∴$\frac{QE}{QB}$=$\frac{DE}{PB}$=$\frac{1}{4}$,
设P(m,-$\frac{1}{4}$m2-2),则B(m,-1),PB=$\frac{1}{4}$m2+1,
∴E点坐标为($\frac{1}{4}$m,-1),D点坐标为[$\frac{1}{4}$m,-$\frac{1}{4}$($\frac{1}{4}$m)2-2],
∴ED=-1+$\frac{1}{4}$($\frac{1}{4}$m)2+2=$\frac{1}{64}$m2+1,
∴$\frac{1}{4}$m2+1=4($\frac{1}{64}$m2+1),解得m1=4,m2=-4,
∴P点坐标为(4,-6)或(-4,-6),
当P点坐标为(4,-6)时,直线PQ的解析式为y=-$\frac{5}{4}$x-1,
当P点坐标为(-4,-6)时,直线PQ的解析式为y=$\frac{5}{4}$x-1,
即直线PQ的解析式为y=$\frac{5}{4}$x-1或y=-$\frac{5}{4}$x-1.
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征和相似三角形的判定与性质;会利用待定系数法求一次函数解析式;理解坐标与图形性质,记住两点间的距离公式.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
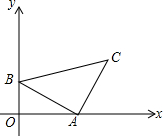 如图,在△ABC中,∠C=45°,∠BAC=90°,点A为($\sqrt{3}$,0)、点B为(0,1),坐标系内有一动点P,使得以P、A、C为顶点的三角形和△ABC全等,则P点坐标为(1,$\sqrt{3}$+1)、(2$\sqrt{3}$,-1)、(2$\sqrt{3}$+1,$\sqrt{3}$-1).
如图,在△ABC中,∠C=45°,∠BAC=90°,点A为($\sqrt{3}$,0)、点B为(0,1),坐标系内有一动点P,使得以P、A、C为顶点的三角形和△ABC全等,则P点坐标为(1,$\sqrt{3}$+1)、(2$\sqrt{3}$,-1)、(2$\sqrt{3}$+1,$\sqrt{3}$-1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
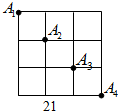 如图,点A1、A2、A3、A4是某市正方形道路网的部分交汇点,且它们都位于同一对角线上.某人从点A1出发,规定向右或向下行走,那么到达点A3的走法共有6种.
如图,点A1、A2、A3、A4是某市正方形道路网的部分交汇点,且它们都位于同一对角线上.某人从点A1出发,规定向右或向下行走,那么到达点A3的走法共有6种.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com