
分析 (1)先利用一次函数图象上点的坐标特征求出B、C的坐标,再利用平移的性质写出A1,B1,C1点坐标,然后描点即可得到△A1B1C1;
(2)利用关于中心对称的点的坐标特征写出A2,B2,C2点坐标,然后描点即可得到△A2B2C2;
(3)利用两点之间线段最短,作C点关于x轴的对称点C′,然后连结C1C′交x轴为P点,则PC+PC1最小,再写出P点坐标;
(4)分类:分别以B、C为圆心,BC为半径画圆交y轴于Q3、Q1、Q4点,作BC的垂直平分线交y轴于Q2,然后写出其中两个点的坐标.
解答 解:(1)把B(1,a),C(2,b)分别代入y=-3x+7中得a=-3+7=4,b=-6+7=1,则B(1,4),C(2,1);
如图,△A1B1C1为所作,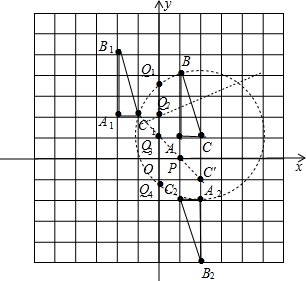 A1的坐标为(-2,2),B1的坐标为(-2,5),C1的坐标为(-1,2);
A1的坐标为(-2,2),B1的坐标为(-2,5),C1的坐标为(-1,2);
(2)如图,△A2B2C2为所作,A2的坐标为(2,-2),B2的坐标为(2,-5),C2的坐标为(1,-2);
(3)如图,点P为所作,P点坐标为(1,0);
(4)如图,点Q1、Q2、Q3、Q4为所作,其中Q2的坐标为(0,2),Q3的坐标为(0,1).
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了等腰三角形的判定和最短路径问题.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:初中数学 来源: 题型:解答题
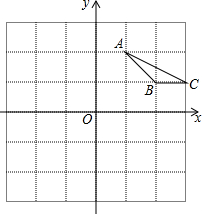 如图,平面直角坐标系中,△ABC的顶点在方格纸的格点处,每个小正方形的边长为单位1.
如图,平面直角坐标系中,△ABC的顶点在方格纸的格点处,每个小正方形的边长为单位1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 宁波、温州两地相距约300千米,一辆火车和一辆轿车先后从宁波出发去温州,设货车行驶的时间为x(小时),如图线段OA、折线BCD分别表示货车、轿车离宁波距离y(千米)与x(小时)之间的函数关系,根据图象解答下列问题:
宁波、温州两地相距约300千米,一辆火车和一辆轿车先后从宁波出发去温州,设货车行驶的时间为x(小时),如图线段OA、折线BCD分别表示货车、轿车离宁波距离y(千米)与x(小时)之间的函数关系,根据图象解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
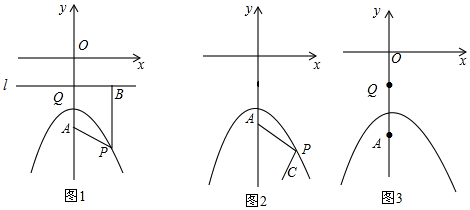
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
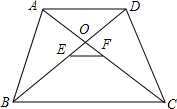 如图:在四边形ABCD中,AD∥BC,AC、BD交于点O,E、F分别是AC、BD的中点,连接E、F,求证:EF∥BC,且EF=$\frac{1}{2}$(BC-AD).
如图:在四边形ABCD中,AD∥BC,AC、BD交于点O,E、F分别是AC、BD的中点,连接E、F,求证:EF∥BC,且EF=$\frac{1}{2}$(BC-AD).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明家有一块三角形的土地,如图所示,其三边长AB=70米,BC=90米,AC=50米,现要把△ABC分成面积比为5:7:9的三部分,分别种植不同的农作物,请你设计一种方案.
小明家有一块三角形的土地,如图所示,其三边长AB=70米,BC=90米,AC=50米,现要把△ABC分成面积比为5:7:9的三部分,分别种植不同的农作物,请你设计一种方案.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com