
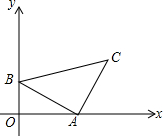
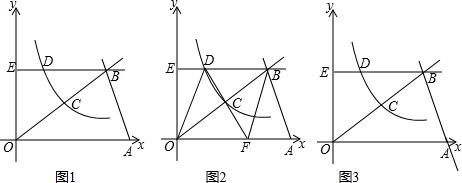
 如图,在△ABC中,∠C=45°,∠BAC=90°,点A为($\sqrt{3}$,0)、点B为(0,1),坐标系内有一动点P,使得以P、A、C为顶点的三角形和△ABC全等,则P点坐标为(1,$\sqrt{3}$+1)、(2$\sqrt{3}$,-1)、(2$\sqrt{3}$+1,$\sqrt{3}$-1).
如图,在△ABC中,∠C=45°,∠BAC=90°,点A为($\sqrt{3}$,0)、点B为(0,1),坐标系内有一动点P,使得以P、A、C为顶点的三角形和△ABC全等,则P点坐标为(1,$\sqrt{3}$+1)、(2$\sqrt{3}$,-1)、(2$\sqrt{3}$+1,$\sqrt{3}$-1). 分析 根据题意得出符合的3种情况:①延长BA到P,使AB=AP;②过点C在点C的一侧作CP⊥AC,使CP=AB;③过点C在点C的另一侧作CP⊥AC,使CP=AB,画出图形,结合图形和全等三角形的性质求出每种情况即可.
解答 解:∵点A坐标为($\sqrt{3}$,0)、点B坐标为(0,1),
∴OA=$\sqrt{3}$,OB=1,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=2
∵∠BAC=90°,∠ACB=45°,
∴AB=AC=2,BC=2$\sqrt{2}$,
△ABC与△ACP全等分为三种情况:
①如图1,延长BA到P,使AB=AP,连接CP,过P作PM⊥x轴于M,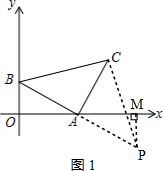
则∠AOB=∠AMP=90°
在△AOB和△AMP中,
∵$\left\{\begin{array}{l}{∠AOB=∠AMP}\\{∠OAB=∠MAP}\\{AB=AP}\end{array}\right.$,
∴△AOB≌△AMP(AAS),
∴AM=AO=$\sqrt{3}$,MP=OB=1,
故点P的坐标为(2$\sqrt{3}$,-1);
②如图2,过点C作CP⊥AC,使CP=AB,则△ABC≌△CPA,
故∠PAC=∠ACB=45°,AP=BC=2$\sqrt{2}$,
过P作PM⊥x轴于M,此时∠PAM=15°,在x轴上取一点N,使∠PNM=30°
∴∠PAM=∠APN=15°,即NA=NP,
设PM=x,则PN=AN=2x,NM=$\sqrt{3}$x,
在RT△APM中,∵AP2=AM2+PM2,
∴(2$\sqrt{2}$)2=(2x+$\sqrt{3}$x)2+x2,解得:x=$\sqrt{3}$-1,
则AM=OA+2x+$\sqrt{3}$x=2$\sqrt{3}$+1,
故点P的坐标为(2$\sqrt{3}$+1,$\sqrt{3}$-1);
③如图3,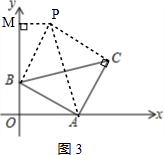
作CP⊥AC,使CP=AB,连接BP,则△ABC≌△CPA,
∵∠BAC=∠PCA=90°,且CP=AB,
∴四边形ABPC是矩形,
∴AB=BP,∠ABP=90°,即∠ABO+∠PBM=90°,
过点P作PM⊥y轴,则∠BPM+∠PBM=90°,
∴∠ABO=∠BPM,
在△AOB和△BMP中,
∵$\left\{\begin{array}{l}{∠AOB=∠BMP}\\{∠ABO=∠BPM}\\{AB=BP}\end{array}\right.$,
∴△AOB≌△BMP(AAS),
∴BM=OA=$\sqrt{3}$,PM=OB=1,
故点P的坐标为(1,$\sqrt{3}+1$);
综上,点P的坐标为(1,$\sqrt{3}$+1),(2$\sqrt{3}$,-1),(2$\sqrt{3}$+1,$\sqrt{3}$-1).
点评 本题考查了全等三角形的性质和判定、勾股定理、含30度角的直角三角形等知识点的应用,注意要进行分类讨论是解题的根本,不遗漏任何一种情况是关键.


科目:初中数学 来源: 题型:填空题
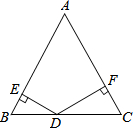 如图,△ABC是等边三角形,点D是BC边上任意一点,DE⊥AB于点E,DF⊥AC于点F,若△ABC的BC边上的高为2,则DE2+2DE•DF+DF2=4.
如图,△ABC是等边三角形,点D是BC边上任意一点,DE⊥AB于点E,DF⊥AC于点F,若△ABC的BC边上的高为2,则DE2+2DE•DF+DF2=4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 宁波、温州两地相距约300千米,一辆火车和一辆轿车先后从宁波出发去温州,设货车行驶的时间为x(小时),如图线段OA、折线BCD分别表示货车、轿车离宁波距离y(千米)与x(小时)之间的函数关系,根据图象解答下列问题:
宁波、温州两地相距约300千米,一辆火车和一辆轿车先后从宁波出发去温州,设货车行驶的时间为x(小时),如图线段OA、折线BCD分别表示货车、轿车离宁波距离y(千米)与x(小时)之间的函数关系,根据图象解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
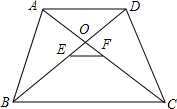 如图:在四边形ABCD中,AD∥BC,AC、BD交于点O,E、F分别是AC、BD的中点,连接E、F,求证:EF∥BC,且EF=$\frac{1}{2}$(BC-AD).
如图:在四边形ABCD中,AD∥BC,AC、BD交于点O,E、F分别是AC、BD的中点,连接E、F,求证:EF∥BC,且EF=$\frac{1}{2}$(BC-AD).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明家有一块三角形的土地,如图所示,其三边长AB=70米,BC=90米,AC=50米,现要把△ABC分成面积比为5:7:9的三部分,分别种植不同的农作物,请你设计一种方案.
小明家有一块三角形的土地,如图所示,其三边长AB=70米,BC=90米,AC=50米,现要把△ABC分成面积比为5:7:9的三部分,分别种植不同的农作物,请你设计一种方案.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com