
���� ��1����ÿ��������ÿ�¿���װx���綯�����¹���ÿ�·ֱ�װy���綯���������ݰ�װ8���綯�����Ͱ�װ14���綯��������������ϵ�г������飬Ȼ����⼴�ɣ�
��2�����������m�ˣ�����һ��İ�װ�����г�����������m��ʾ��n��Ȼ���������m������������⼴�ɣ�
��3������������ϵʽ������ʹ�¹��˵�����������������ͬʱ����ÿ��֧���Ĺ����ܶ�W��Ԫ�������ܵ��٣������������з�����
��� �⣺��1����ÿ����������ÿ�¿���װx���綯������ÿ���¹���ÿ�¿���װy���綯������
�������⣬�ã�$\left\{\begin{array}{l}{x+2y=8}\\{2x+3y=14}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{x=4}\\{y=2}\end{array}\right.$��
��ÿ����������ÿ�¿���װ4���綯������ÿ���¹���ÿ�¿���װ2���綯������
��2���蹤�����m����������װ�綯������
��48m+24n=240����n=10-2m��
��0��n��10��
��0��10-2m��10����ã�0��m��5��
����Ƹ����������4�֣��ٳ��1��������ʱ����Ƹ8���¹��ˣ��ڳ��2��������ʱ����Ƹ6���¹��ˣ��۳��3��������ʱ����Ƹ4���¹��ˣ��ܳ��4��������ʱ����Ƹ2���¹��ˣ�
��3���������⣬����ÿ��֧���Ĺ����ܶ�W=2000m+1200��10-2m��=-400m+12000��
��-400��0��
��W��x�����������
�֡�10-2m��m��
��m��$\frac{10}{3}$��
�ʵ�m=3ʱ����n=4ʱ��Wȡ����Сֵ��
�𣺹���Ӧ��Ƹ4���¹��ˣ���ʹ�¹��˵�����������������ͬʱ����ÿ��֧���Ĺ����ܶ���ܵ��٣�
���� ������Ҫ���鷽�̡������顢����ʽ��һ�κ�����Ӧ�ã�����Ҫ�ܹ��������⣬��ȷ�ҵ�������ϵ�Ͳ��ȹ�ϵ�������ⷽ�������������������ʽ��δ֪����ֵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{x-1}{{{x^2}-3x+2}}$ | B�� | $\frac{1}{x+1}$ | C�� | $\frac{2x-2}{x-2}$ | D�� | $\frac{x+2}{x-1}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
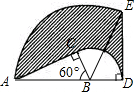 ��ͼ����ABC�У���C��ֱ�ǣ�AB=6cm����ABC=60�㣬����ABC�Ե�BΪ����˳ʱ����ת��ʹ��C��ת��AB���ӳ����ϵ�D������AC��ɨ����ͼ��������Ӱ���ֵ������9�У�
��ͼ����ABC�У���C��ֱ�ǣ�AB=6cm����ABC=60�㣬����ABC�Ե�BΪ����˳ʱ����ת��ʹ��C��ת��AB���ӳ����ϵ�D������AC��ɨ����ͼ��������Ӱ���ֵ������9�У��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
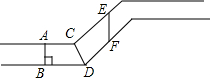 һ����·�Ķ���ͼ��ʾ��ͼ�������߶εij����ܱȽ�ȷ�е�������һ�ι�·�Ŀ��ȣ���˵�����ɣ�
һ����·�Ķ���ͼ��ʾ��ͼ�������߶εij����ܱȽ�ȷ�е�������һ�ι�·�Ŀ��ȣ���˵�����ɣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
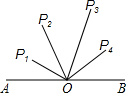 ��ͼ��OΪ�߶�AB���е㣬AB=4cm��P1��P2��P3��P4����O�ľ���ֱ���1cm��2cm��2.8cm��1.7cm�������ĵ�������A��B����ֱ�������εĶ����ǣ�������
��ͼ��OΪ�߶�AB���е㣬AB=4cm��P1��P2��P3��P4����O�ľ���ֱ���1cm��2cm��2.8cm��1.7cm�������ĵ�������A��B����ֱ�������εĶ����ǣ�������| A�� | P1 | B�� | P2 | C�� | P3 | D�� | P4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com