
Ζ÷Έω Θ®1Θ©ΙιΡ…ΉήΫαΒΟΒΫ≤πœνΙφ¬…Θ§ΫΪ‘≠ Ϋ±δ–ΈΚσΦΤΥψΦ¥Ω…ΒΟΒΫΫαΙϊΘΜ
Θ®2Θ©άϊ”ΟΒΟ≥ωΒΡ≤πœνΙφ¬…ΫΪΖΫ≥Χ±δ–ΈΘ§«σ≥ωΫβΘ§Φλ―ιΦ¥Ω…Θ°
Ϋβ¥π ΫβΘΚΘ®1Θ©‘≠ Ϋ=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+Γ≠+$\frac{1}{n}$-$\frac{1}{n+1}$=1-$\frac{1}{n+1}$=$\frac{n}{n+1}$ΘΜ
Θ®2Θ©ΖΫ≥Χ’ϊάμΒΟΘΚ$\frac{1}{x+2}$-$\frac{1}{x+3}$+$\frac{1}{x+3}$-$\frac{1}{x+4}$+Γ≠+$\frac{1}{x+2013}$-$\frac{1}{x+2014}$=$\frac{x}{Θ®x+2Θ©Θ®x+2014Θ©}$Θ§
Φ¥$\frac{2012}{Θ®x+2Θ©Θ®x+2014Θ©}$=$\frac{x}{Θ®x+2Θ©Θ®x+2014Θ©}$Θ§
»ΞΖ÷ΡΗΒΟΘΚx=2012Θ§
Ψ≠Φλ―ιx=2012 «Ζ÷ ΫΖΫ≥ΧΒΡΫβΘ°
Ι ¥πΑΗΈΣΘΚΘ®1Θ©$\frac{n}{n+1}$
ΒψΤά ¥ΥΧβΩΦ≤ιΝΥΫβΖ÷ ΫΖΫ≥ΧΘ§ΫβΖ÷ ΫΖΫ≥ΧΒΡΜυ±ΨΥΦœκ «ΓΑΉΣΜ·ΥΦœκΓ±Θ§Α―Ζ÷ ΫΖΫ≥ΧΉΣΜ·ΈΣ’ϊ ΫΖΫ≥Χ«σΫβΘ°ΫβΖ÷ ΫΖΫ≥Χ“ΜΕ®ΉΔ“β“Σ―ιΗυΘ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
 »γΆΦΘ§‘Ύ10ΓΝ6ΒΡΆχΗώ÷–Θ§ΟΩΗω–Γ’ΐΖΫ–ΈΒΡ±Ώ≥ΛΕΦΈΣ1Θ§ΟΩΗω–Γ’ΐΖΫ–ΈΒΡΕΞΒψ≥ΤΈΣΗώΒψΘ§ΓςAOBΒΡΕΞΒψΕΦ‘ΎΗώΒψ…œΘ§«“OΒψ «÷±Ϋ«Ήχ±ξœΒΒΡ‘≠ΒψΘ°
»γΆΦΘ§‘Ύ10ΓΝ6ΒΡΆχΗώ÷–Θ§ΟΩΗω–Γ’ΐΖΫ–ΈΒΡ±Ώ≥ΛΕΦΈΣ1Θ§ΟΩΗω–Γ’ΐΖΫ–ΈΒΡΕΞΒψ≥ΤΈΣΗώΒψΘ§ΓςAOBΒΡΕΞΒψΕΦ‘ΎΗώΒψ…œΘ§«“OΒψ «÷±Ϋ«Ήχ±ξœΒΒΡ‘≠ΒψΘ°≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
 »γΆΦΘ§‘ΎΓςABC÷–Θ§BC=5Θ§AC=8Θ§ABΒΡ¥Ι÷±ΤΫΖ÷œΏΫΜAB”ΎΒψDΘ§ΫΜAC”ΎΒψEΘ§‘ρΓςBCEΒΡ÷ή≥ΛΒ»”ΎΘ®ΓΓΓΓΘ©
»γΆΦΘ§‘ΎΓςABC÷–Θ§BC=5Θ§AC=8Θ§ABΒΡ¥Ι÷±ΤΫΖ÷œΏΫΜAB”ΎΒψDΘ§ΫΜAC”ΎΒψEΘ§‘ρΓςBCEΒΡ÷ή≥ΛΒ»”ΎΘ®ΓΓΓΓΘ©| AΘ° | 18 | BΘ° | 15 | CΘ° | 13 | DΘ° | 12 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
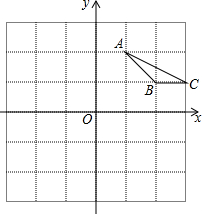 »γΆΦΘ§ΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§ΓςABCΒΡΕΞΒψ‘ΎΖΫΗώ÷ΫΒΡΗώΒψ¥ΠΘ§ΟΩΗω–Γ’ΐΖΫ–ΈΒΡ±Ώ≥ΛΈΣΒΞΈΜ1Θ°
»γΆΦΘ§ΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§ΓςABCΒΡΕΞΒψ‘ΎΖΫΗώ÷ΫΒΡΗώΒψ¥ΠΘ§ΟΩΗω–Γ’ΐΖΫ–ΈΒΡ±Ώ≥ΛΈΣΒΞΈΜ1Θ°≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | -1 | BΘ° | 1 | CΘ° | 2 | DΘ° | 3 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com