
【题目】某市教育行政部门为了了解初一学生每学期参加综合实践活动的情况,随机抽样调查了某校初一学生一个学期参加综合实践活动的天数,并用得到的数据绘制了下面两幅不完整的统计图,请你根据图中提供的信息,回答下列问题:

(1)扇形统计图中a的值为_____,“活动时间为4天”的扇形所对圆心角的度数为_____°,该校初一学生的总人数为______;
(2)补全频数分布直方图;
(3)如果该市共有初一学生6000人,请你估计“活动时间不少于4天”的大约有多少人?
【答案】(1)25%;108;200(2)见解析(3)4500
【解析】
(1)由条形统计图可知“活动时间为3天”与“活动时间为6天”的人数相同,可得“活动时间为6天”的所占百分比,即可求出a的值;根据“活动时间为4天”的所占百分比乘以360°即可得答案;根据“活动时间为4天”的人数为60人,占总数30% 即可计算总人数;(2)用总人数乘以a即可得“活动时间为5天”的人数,补全统计图即可;(3)根据样本估计总体.
(1)∵“活动时间为3天”与“活动时间为6天”的人数相同,
∴“活动时间为6天”的所占百分比为15%,
∴a=1-30%-15%-10%-5%-15%=25%,
360°×30%=108°,
60÷30%=200(人)
故答案为:25%;108;200
(2)200×25%=50(人),
故“活动时间为5天”的人数为50人,补全频数分布直方图如下:
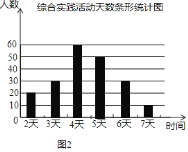
(3)6000×(30%+25%+15%+5%)=4500(人)
答:该市活动时间不少于4天的人数约是4500人.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】乘法公式的探究与应用:
(1)如图甲,边长为a的大正方形中有一个边长为b的小正方形,请你写出阴影部分的面积是
(2)小颗将阴影部分接下来,重新拼成一个长方形,如图乙,则长方形的长是 ,宽是 ,面积是 (写成多项式乘法的形式).
(3)比较甲乙两图阴影部分的面积,可以得到恒等式
(4)运用你所得到的公式计算:10.3×9.7.
(5)若49x2﹣y2=25,7x﹣y=5,则7x+y的值为

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一段抛物线y=﹣x(x﹣3)(0≤x≤3),记为C1 , 它与x轴交于点O,A1;将C1绕点A1旋转180°得C2 , 交x 轴于点A2;将C2绕点A2旋转180°得C3 , 交x 轴于点A3;…如此进行下去,得到一条“波浪线”.若点P(37,m)在此“波浪线”上,则m的值为 . 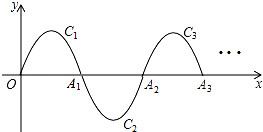
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,点
,点![]() 为平面内一点.
为平面内一点.
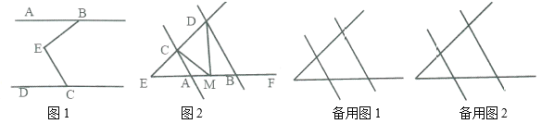
(1)如图1,![]() 和
和![]() 互余,小明说过
互余,小明说过![]() 作
作![]() ,很容易说明
,很容易说明![]() 。请帮小明写出具体过程;
。请帮小明写出具体过程;
(2)如图2,![]() ,当点
,当点![]() 在线段
在线段![]() 上移动时(点
上移动时(点![]() 与
与![]() ,
,![]() 两点不重合),指出
两点不重合),指出![]() 与
与![]() ,
,![]() 的数量关系?请说明理由;
的数量关系?请说明理由;
(3)在(2)的条件下,若点![]() 在
在![]() ,
,![]() 两点外侧运动(点
两点外侧运动(点![]() 与
与![]() ,
,![]() ,
,![]() 三点不重合)请直接写出
三点不重合)请直接写出![]() 与
与![]() ,
,![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
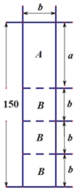
【题目】装饰公司为小明家设计电视背景墙时需要A、B型板材若干块,A型板材规格是ab,B型板材规格是bb.现只能购得规格是150b的标准板材.(单位:cm)
(1)若设a60cm,b30cm.一张标准板材尽可能多的裁出A型、B型板材,共有下表三种裁法,下图是裁法一的裁剪示意图.
裁法一 | 裁法二 | 裁法三 | |
A型板材块数 | 1 | 2 | 0 |
B型板材块数 | 3 | m | n |
则上表中, m=___________, n=__________;
(2)为了装修的需要,小明家又购买了若干C型板材,其规格是aa,并做成如下图的背景墙.请写出下图中所表示的等式:__________;
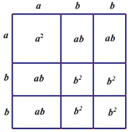
(3)若给定一个二次三项式2a25ab3b2,试用拼图的方式将其因式分解.(请仿照(2)在几何图形中标上有关数量)
查看答案和解析>>
科目:初中数学 来源: 题型:
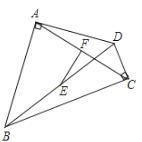
【题目】如图,四边形ABCD中,∠BAD=90°,∠DCB=90°,EF分别是BD、AC的中点,
(1)请你猜测EF与AC的位置关系,并给予证明;
(2)当AC=8,BD=10时,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有3个完全相同的小球,把它们分别标号为1,2,3,放在一个不透明的口袋中,从口袋中随机摸出一个小球,记下标号后放回,再从口袋中随机摸出一个小球,记下标号.用画树状图(或列表)的方法,求两次摸出的小球号码恰好都大于1的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
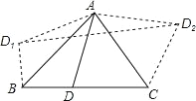
【题目】如图,在△ABC中,∠ABC=45°,∠ACB=60°,BC=2![]() +2,D是BC边上异于点B,C的一动点,将三角形ABD沿AB翻折得到△ABD1,将△ACD沿AC翻折得到△ACD2,连接D1D2,则四边形D1BCD2的面积的最大值是_____.
+2,D是BC边上异于点B,C的一动点,将三角形ABD沿AB翻折得到△ABD1,将△ACD沿AC翻折得到△ACD2,连接D1D2,则四边形D1BCD2的面积的最大值是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com