
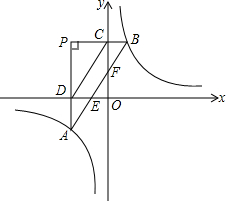
 如图,将透明三角形纸片PAB的直角顶点P落在第二象限,顶点A、B分别落在反比例函数y=$\frac{k}{x}$图象的两支上,且PB⊥y轴于点C,PA⊥x轴于点D,AB分别与x轴、y轴相交于点E、F.已知B(1,3).
如图,将透明三角形纸片PAB的直角顶点P落在第二象限,顶点A、B分别落在反比例函数y=$\frac{k}{x}$图象的两支上,且PB⊥y轴于点C,PA⊥x轴于点D,AB分别与x轴、y轴相交于点E、F.已知B(1,3).分析 (1)把B坐标代入反比例解析式求出k的值即可;
(2)由题意表示出P,D,C,A的坐标,求出两对应边之比,再由夹角相等,利用两边对应边对应成比例且夹角相等的三角形相似得到三角形PDC与三角形PAB相似,进而得出四边形ADCF与四边形DEBC都是平行四边形,利用平行四边形的对边相等即可得证;
(3)由四边形ABCD面积等于三角形PAB面积减去三角形PCD面积,列出关于m的方程,求出方程的解得到m的值,即可确定出P的坐标.
解答 解:(1)把B(1,3)代入反比例解析式得:k=3;
故答案为:3;
(2)根据题意得:P(m,3),D(m,0),C(0,3),A(m,$\frac{3}{m}$),
∵$\frac{PC}{PB}$=$\frac{-m}{1-m}$=$\frac{m}{m-1}$,$\frac{PD}{PA}$=$\frac{3}{3-\frac{3}{m}}$=$\frac{m}{m-1}$,
∴$\frac{PC}{PB}$=$\frac{PD}{PA}$,
又∵∠P=∠P,
∴△PDC∽△PAB,∠PDC=∠PAB,
∴DC∥AB,
又∵AD∥CF,DE∥CB,
∴四边形ADCF和四边形DEBC都是平行四边形,
∴AF=DC,DC=BE,
∴AF=BE,
∴AE=BF;
(3)由S四边形ABCD=S△APB-S△PCD=$\frac{1}{2}$PA•PB-$\frac{1}{2}$PC•PD=$\frac{1}{2}$(3-$\frac{3}{m}$)(1-m)-$\frac{1}{2}$×3(-m)=4,
解得:m=-$\frac{3}{2}$,
则P(-$\frac{3}{2}$,3).
点评 此题属于反比例函数综合题,涉及的知识有:待定系数法求反比例函数解析式,坐标与图形性质,平行四边形的判定与性质,以及相似三角形的判定与性质,熟练掌握相似三角形的判定与性质是解本题第二问的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com