
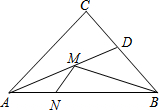
 如图,在锐角△ABC中,AB=6,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是( )
如图,在锐角△ABC中,AB=6,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是( )| A. | $3\sqrt{2}$ | B. | 4 | C. | $4\sqrt{2}$ | D. | 6 |
分析 作BH⊥AC,垂足为H,交AD于M点,过M点作MN⊥AB,垂足为N,则BM+MN为所求的最小值,根据AD是∠BAC的平分线可知MH=MN,再由锐角三角函数的定义即可得出结论.
解答 解:如图,作BH⊥AC,垂足为H,交AD于M点,过M点作MN⊥AB,垂足为N.
∵AD是∠BAC的平分线,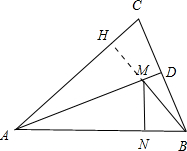
∴MH=MN,
∴BM+MN=BM+MH=BN,
∴BH是点B到直线AC的最短距离(垂线段最短),
∴BH就是BM+MN的最小值,
∵AB=6,∠BAC=45°,
∴BH=AB•sin45°=6×$\frac{\sqrt{2}}{2}$=3$\sqrt{2}$.
∴BM+MN的最小值是3$\sqrt{2}$.
故选A.
点评 本题考查的是轴对称-最短路线问题,解答此类问题时要从已知条件结合图形认真思考,通过角平分线性质,垂线段最短,确定线段和的最小值.


科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 10 | C. | 12 | D. | 20 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
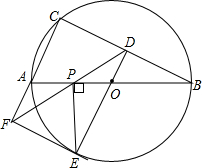 如图,⊙O是△ABC的外接圆,AB是直径,过点O作OD⊥CB,垂足为点D,延长DO交⊙O于点E,过点E作PE⊥AB,垂足为点P,作射线DP交CA的延长线于F点,连接EF,
如图,⊙O是△ABC的外接圆,AB是直径,过点O作OD⊥CB,垂足为点D,延长DO交⊙O于点E,过点E作PE⊥AB,垂足为点P,作射线DP交CA的延长线于F点,连接EF,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
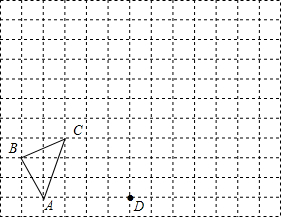 如图,在由边长为1的单位正方形组成的网格中,按要求画出坐标系及△A1B1C1及△A2B2C2;
如图,在由边长为1的单位正方形组成的网格中,按要求画出坐标系及△A1B1C1及△A2B2C2;查看答案和解析>>
科目:初中数学 来源: 题型:选择题
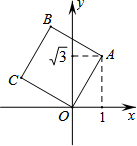 如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1,$\sqrt{3}$),则点C的坐标为( )
如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1,$\sqrt{3}$),则点C的坐标为( )| A. | (-1,$\sqrt{3}$) | B. | (-$\sqrt{3}$,1) | C. | (-2,1) | D. | (-1,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com