练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    13．已知y与x2成正比例，且当x=3时，y=-18，写出y与x之间的函数解析式，它是二次函数吗？

    分析 由于y与x2成反比例，则有y=kx2（k≠0），然后把x=3，y=-18代入即可求出k．

    解答 解：∵y与x2成正比例，
    ∴y=kx2（k≠0），
    把x=3时，y=-18代入得：-18=32•k，
    ∴k=-2，
    ∴y与x之间的函数解析式为 y=-2x2．
    符合二次函数的定义，属于二次函数．

    点评 本题考查了二次函数的定义，正比例函数的定义．二次函数的定义：一般地，形如y=ax2+bx+c（a、b、c是常数，a≠0）的函数，叫做二次函数．其中x、y是变量，a、b、c是常量，a是二次项系数，b是一次项系数，c是常数项．y=ax2+bx+c（a、b、c是常数，a≠0）也叫做二次函数的一般形式．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    3．把多项式2x2-18分解因式，结果正确的是（　　）
    A．2（x2-9）B．2（x+9）（x-9）C．2（x+3）（x-3）D．2（x-3）2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

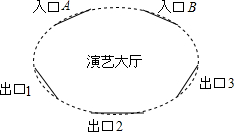    4．某演艺大厅有2个入口和3个出口，其示意图如下，参观者从任意一个入口进入，参观结束后从任意一个出口离开
    （1）用树状图表示，小明从进入到离开，对于入口和出口的选择有多少种不同的结果？
    （2）小明从入口A进入并从出口1离开的概率是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

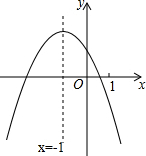    1．二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列结论：
    ①b2-4ac＞0；
    ②4a+c＞2b；
    ③（a+c）2＞b2；
    ④x（ax+b）≤a-b．
    其中正确结论的是①②④．（请把正确结论的序号都填在横线上）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

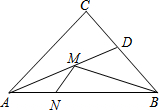    8．如图，在锐角△ABC中，AB=6，∠BAC=45°，∠BAC的平分线交BC于点D，M、N分别是AD和AB上的动点，则BM+MN的最小值是（　　）
    A．$3\sqrt{2}$B．4C．$4\sqrt{2}$D．6

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．漳州市教育局到某校抽查七年级学生“根据音标写单词”的水平，随机抽取若干名学生进行测试（成绩取整数，满分为100分）．如下两幅是尚未绘制完整的统计图，请根据图中提供的信息，解答下列问题：

    （1）本次抽取的学生有50人；
    （2）该年段有450名学生，若全部参加测试，请估计60分以上（含60分）有432人；
    （3）甲、乙、丙是该校三名英语成绩优秀的学生，随机抽取其中两名学生介绍英语学习经验，请用树状图或列表法表示所有可能的结果，并求抽到甲、乙两名学生的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．在学过了二元一次方程组的解法后，课堂上老师又写出了一个题目：$\left\{\begin{array}{l}{\frac{x+y}{6}+\frac{x-y}{10}=3①}\\{\frac{x+y}{6}-\frac{x-y}{10}=-1②}\end{array}\right.$，你会解这个方程组吗？
    小明、小刚、小芳争论了一会儿，他们分别写出了一种方法：
    小明：把原方程组整理得$\left\{\begin{array}{l}{8x+2y=90③}\\{2x+8y=-30④}\end{array}\right.$
    ④×4-③得30y=-210，所以y=-7
    把y=-7代入③得8x=104，所以x=13，
    即$\left\{\begin{array}{l}{x=13}\\{y=-7}\end{array}\right.$
    小刚：设$\frac{x+y}{6}$=m，$\frac{x-y}{10}$=n，则$\left\{\begin{array}{l}{m+n=3③}\\{m-n=-1④}\end{array}\right.$
    ③+④得m=1，
    ③-④得m=2，
    即$\left\{\begin{array}{l}{\frac{x+y}{6}=1}\\{\frac{x-y}{10}=2}\end{array}\right.$，所以$\left\{\begin{array}{l}{x+y=6}\\{x-y=20}\end{array}\right.$，所以$\left\{\begin{array}{l}{x=13}\\{y=-7}\end{array}\right.$．
    小芳：①+②得$\frac{2（x+y）}{6}$=2，即x+y=6．③
    ①-②得$\frac{2（x-y）}{10}$=4，即x-y=20．④
    ③④组成方程组得x=13
    ③-④得y=-7，即$\left\{\begin{array}{l}{x=13}\\{y=-7}\end{array}\right.$．
    老师看过后，非常高兴，特别是小刚的方法独特，像小刚的这种方法叫做换元法，你能用换元法解下列方程组吗？
    $\left\{\begin{array}{l}{\frac{3x-2y}{6}+\frac{2x+3y}{7}=1}\\{\frac{3x-2y}{6}-\frac{2x+3y}{7}=5}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．一个直角三角形两条直角边的长分别为4，8，另一个和它相似的直角三角形的一条直角边为12，则另一条直角边的长为（　　）
    A．6B．24C．6或24D．6$\sqrt{5}$或$\sqrt{10}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    3．若实数x满足x-$\frac{1}{x}$=1，则$\frac{{x}^{2}}{{x}^{4}+{x}^{2}+1}$的值是（　　）
    A．$\frac{1}{3}$B．$\frac{1}{4}$C．$\frac{1±\sqrt{5}}{2}$D．$\frac{1+\sqrt{5}}{2}$

    查看答案和解析>>

    同步练习册答案