
���� ��$\frac{3x-2y}{6}$=m��$\frac{2x+3y}{7}$=n�����������������m��n��ֵ������ȷ����x��y��ֵ��
��� �⣺��$\frac{3x-2y}{6}$=m��$\frac{2x+3y}{7}$=n��
�����������ã�$\left\{\begin{array}{l}{m+n=1��}\\{m-n=5��}\end{array}\right.$��
��+�ڵã�2m=6����m=3��
��-�ڵã�2n=-4����n=-2��
��$\left\{\begin{array}{l}{\frac{3x-2y}{6}=3}\\{\frac{2x+3y}{7}=-2}\end{array}\right.$��
�����ã�$\left\{\begin{array}{l}{3x-2y=18}\\{2x+3y=-14}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{x=2}\\{y=-6}\end{array}\right.$��
���� ���⿼���˽��Ԫһ�η����飬��������Ԫ��˼�룬��Ԫ�ķ����У�������Ԫ����Ӽ���Ԫ����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
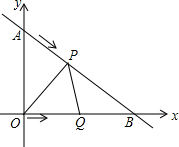 ��ͼ����ƽ��ֱ������ϵ�У�ֱ��y=-$\frac{3}{4}$x+3�������ύ��A��B���㣬��P��Q�ֱ�ΪAB�ߣ�OB���ϵĶ��㣬����ͬʱ�ֱ�ӵ�A����O��ÿ��1����λ�ٶ����յ�B�����ƶ�����һ���㵽���յ�ʱ��һ����Ҳֹͣ�ƶ������ƶ�ʱ��Ϊt�룮
��ͼ����ƽ��ֱ������ϵ�У�ֱ��y=-$\frac{3}{4}$x+3�������ύ��A��B���㣬��P��Q�ֱ�ΪAB�ߣ�OB���ϵĶ��㣬����ͬʱ�ֱ�ӵ�A����O��ÿ��1����λ�ٶ����յ�B�����ƶ�����һ���㵽���յ�ʱ��һ����Ҳֹͣ�ƶ������ƶ�ʱ��Ϊt�룮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
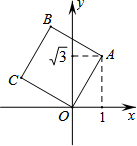 ��ͼ����������OABC����ƽ��ֱ������ϵ�У�O��ԭ�㣬A������Ϊ��1��$\sqrt{3}$�������C������Ϊ��������
��ͼ����������OABC����ƽ��ֱ������ϵ�У�O��ԭ�㣬A������Ϊ��1��$\sqrt{3}$�������C������Ϊ��������| A�� | ��-1��$\sqrt{3}$�� | B�� | ��-$\sqrt{3}$��1�� | C�� | ��-2��1�� | D�� | ��-1��2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com