
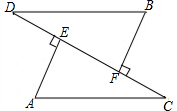
 已知,AC=BD,AE⊥DC于E,BF⊥DC于F,AE=BF.求证:DE=CF.
已知,AC=BD,AE⊥DC于E,BF⊥DC于F,AE=BF.求证:DE=CF.  培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
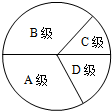 为了解我县1800名初中毕业生参加云南省数学学业水平考试的成绩情况(得分取整数),我们随机抽取了部分学生的数学成绩,将其等级情况制成不完整的统计表如下:
为了解我县1800名初中毕业生参加云南省数学学业水平考试的成绩情况(得分取整数),我们随机抽取了部分学生的数学成绩,将其等级情况制成不完整的统计表如下:| 等级 | A级(优秀) (≥108分) | B级(良好) (≥84分且<108分) | C级(及格) (≥72分且<84分) | D级(不及格) (<72分) |
| 人数 | 22 | 28 | 18 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com