
����Ŀ����֪��P�Ǿ���ABCD��AB�ϵ�����һ�㣨���A��B���غϣ�
��1����ͼ�����ֽ���PBC��PC���۵õ���PEC������AD��ȡһ��F������PAF��PF���۵õ���PGF����ʹ������PE��PG�غϣ�����FG��CE��λ�ù�ϵ��Σ���˵�����ɣ�
��2���ڣ�1���У���ͼ��������FC��ȡFC���е�H������GH��EH������̽���߶�GH���߶�EH�Ĵ�С��ϵ����˵��������ɣ�
��3����ͼ�����ֱ���AD��BC��ȡ��F��C����ʹ����APF=��BPC�����루1���еIJ��������ƣ�������PAF��PF���۵õ���PFG��������![]() ��
��![]() ���۵õ���
���۵õ���![]() ������
������![]() ��ȡ
��ȡ![]() ���е�H������GH��EH�����ʣ�2���еĽ��ۻ���������˵�����ɣ�
���е�H������GH��EH�����ʣ�2���еĽ��ۻ���������˵�����ɣ�

���𰸡���1��FG��CE���ھ���ABCD�У���A=��B=90�㣬������ã���G=��A=90�㣬��PEC=��B=90�㣬���GEC=90�㣬���G=��GEC����FG��CE��
��2��GH=EH���ӳ�GH��CE�ڵ�M���ɣ�1���ã�FG��CE�����GFH=��MCH����HΪCF���е㣬��FH=CH���֡ߡ�GHF=��MHC�����GFH�ա�MHC����GH=HM=![]() ���ߡ�GEC=90�㣬��EH=
���ߡ�GEC=90�㣬��EH=![]() ����GH=EH��
����GH=EH��
��3����2���еĽ��ۻ�������ȡPF���е�M��![]() ���е�N���ߡ�FGP=90�㣬MΪPF���е㣬��
���е�N���ߡ�FGP=90�㣬MΪPF���е㣬��![]() ��
��![]() ��
��![]() ��
��![]() ����GM=PM�����GPF=��MGP�����GMF=��GPF+��MGP=2��GPF����HΪ
����GM=PM�����GPF=��MGP�����GMF=��GPF+��MGP=2��GPF����HΪ![]() ���е㣬MΪPF���е㣬��
���е㣬MΪPF���е㣬��![]() ��ͬ��
��ͬ��![]() ��
��![]() ��HN��PF����
��HN��PF����![]() ����GM=HN��HM=EN���ߡ�GPF=��FPA��
����GM=HN��HM=EN���ߡ�GPF=��FPA��![]() ����
����![]() �����GPF=
�����GPF=![]() �����GMF=��
�����GMF=��![]() ����
����![]() ��
��![]() ��HN��PF�����ı���HMPNΪƽ���ı��Σ����HMF=��
��HN��PF�����ı���HMPNΪƽ���ı��Σ����HMF=��![]() �����GMH=��HNE����GM=HN��HM=EN�����GMH�ա�HNE����GH=HE��
�����GMH=��HNE����GM=HN��HM=EN�����GMH�ա�HNE����GH=HE��
����������1�����ݾ��ε������Լ���ԳƵ����ʿ��Եõ���G=��GEC=90���������ڴ�����ȣ�����֤����
��ֱ��ƽ�У�
�ӳ�GH��CE�ڵ�M����ϣ�1���еĽ���֤����GFH�ա�MHC��������ֱ��������б���ϵ����ߵ���
б�ߵ�һ�����֤�����ۣ�
ȡPF���е�M��PC'���е�N������ֱ�������ε�б���ϵ����ߵ���б�ߵ�һ���Լ������ε���λ��
�����õ�ƽ���ı��Σ��⼸��ƽ���ı��ε�����֤��Ҫ֤���������߶����ڵ�����������ȫ�ȣ��Ӷ�֤�����ۣ�


 �����߿����ϵ�д�
�����߿����ϵ�д� �㾦�½̲�ȫ�ܽ��ϵ�д�
�㾦�½̲�ȫ�ܽ��ϵ�д� Сѧ�̲���ȫ���ϵ�д�
Сѧ�̲���ȫ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪A��B���������������20�ף�A���������ϱ�ʾ�ĵ�Ϊ-8��С�ڹ��A�س�����������B�ط���ǰ������һ��ǰ��1�ף��ڶ��κ���2�ף���������ǰ��3�ף����Ĵ��ֺ���4�ף����������˹����н����������һ����λ���ȵ���1�ף�
![]()
��1����B���������ϱ�ʾ������
��2����B����ԭ�����࣬����������н���С�ڹ굽���P���������н����Q�����P�͵�Q����A�ľ����������˵�����ɣ�
��3����B����ԭ����Ҳ࣬��ô����30���н���С�ڹ굽��ĵ����B֮��ľ����Ƕ����ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����ABCD�У���E��BC���е㣬����AE���ӳ���DC���ӳ����ڵ�F������BF��
(1)��֤����ABE�ա�FCE��
(2)��AF��AD����֤���ı���ABFC�Ǿ��Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵���У���ȷ�ĸ����У�������
����ֱ֪�������ε����Ϊ2����ֱ�DZߵı�Ϊ1��2����б�߳�Ϊ![]() ��
��
��ֱ�������ε����߳�Ϊ![]() ����̱߳�Ϊ1������һ�߳�Ϊ
����̱߳�Ϊ1������һ�߳�Ϊ![]() ��
��
���ڡ�ABC�У�����A����B����C=1��5��6�����ABCΪֱ�������Σ�
�ܵ������������Ϊ12���ױ��ϵĸ�Ϊ4��������Ϊ5��
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����ϵ�A��B����ֱ��Ӧ����a��b����a��b����|4a-b|+��a-4��2=0
![]()
��1��a= ��b= ���������������A��B���㣻
��2������P�ӵ�A��������ÿ��3����λ������x���������˶������˶�ʱ��Ϊ����ʱ����P����A�ľ����ǵ�P����B�����2����
��3�������ϻ���һ��C������Ϊ30������P�͵�Qͬʱ�ӵ�A�͵�B�������ֱ���ÿ��3����λ���Ⱥ�ÿ��1����λ���ȵ��ٶ���C���˶���P�㵽��C�����������ͬ�����ٶȷ��أ��˶����յ�A�����P�͵�Q�˶�������ʱ��P��Q����֮��ľ���Ϊ4�������ʱ��Q��Ӧ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ͼ���ṩ����Ϣ���ش��������⣺

��1��һ��ˮƿ��һ��ˮ���ֱ��Ƕ���Ԫ��
��2���ס��������̳�ͬʱ����ͬ����ˮƿ��ˮ����Ϊ��ӭ�����꣬�����̳����ڸ����������̳��涨����������Ʒ������ۣ����̳��涨����һ��ˮƿ��������ˮ����������ˮ����ԭ��������ij��λ��Ҫ��5��ˮƿ��20��ˮ��������ѡ���ļ��̳���������㣬��˵�����ɣ���������ͬһ�ҹ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC��BA=BC����D��AB�ӳ�����һ�㣬DF��AC��F��BC��E��
��֤����DBE�ǵ��������Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ����ϣ���ʦ�������ɸ���ͼ1������ֽƬ��A��ֽƬ�߳�Ϊa�������Σ�B��ֽƬ�DZ߳�Ϊb�������Σ�C��ֽƬ��Ϊa����Ϊb�ij����Σ�����A��ֽƬһ�ţ�B��ֽƬ�ţ�C��ֽƬ����ƴ����ͼ2�Ĵ������Σ�

��1���������ֲ�ͬ�ķ�����ͼ2�������ε������
����1���� ��������2���� ��
��2���۲�ͼ2������д��������������ʽ����a+b��2��a2+b2��ab֮��ĵ�����ϵ���� ��
��3�����ݣ�2�����еĵ�����ϵ������������⣺
����֪��a+b=5��a2+b2=11����ab��ֵ��
����֪��2018��a��2+��a��2017��2=5����2018��a����a��2017����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
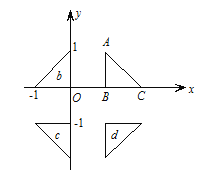
����Ŀ����ͼ������ֱ��������![]() �ֱ�����ij��ֱ�߶ԳƵõ�ͼ��
�ֱ�����ij��ֱ�߶ԳƵõ�ͼ��![]() ���������Գƹ�ϵ���ֲ��䣬ƽ��
���������Գƹ�ϵ���ֲ��䣬ƽ��![]() ��ʹ���ĸ�ͼ���ܹ�Χ��һ�����ص�����϶�������Σ���ʱ��
��ʹ���ĸ�ͼ���ܹ�Χ��һ�����ص�����϶�������Σ���ʱ��![]() ������������εı߳�Ϊ�� ��
������������εı߳�Ϊ�� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com