
分析 先根据判别式的意义可判断m<$\frac{3}{4}$,再根据根与系数的关系得到α+β=-(2m-3),αβ=m2,接着由$\frac{α}{β}$+$\frac{β}{α}$=-1变形得到(α+β)2=αβ,则(2m-3)2=m2,解得m=3或m=1,然后根据m<$\frac{3}{4}$,可判断m无实数值.
解答 解:根据题意得△=(2m-3)2-4m2>0,解得m<$\frac{3}{4}$,
α+β=-(2m-3),αβ=m2,
∵$\frac{α}{β}$+$\frac{β}{α}$=-1,
∴α2+β2=-αβ,
∴(α+β)2=αβ,
∴(2m-3)2=m2,解得m=3或m=1,
∵m<$\frac{3}{4}$,
∴m无解.
故答案为无实数值.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 2$\sqrt{3}$ | D. | 2$\sqrt{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
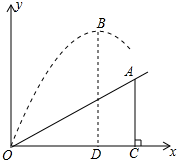 如图,小明在一次高尔夫球争霸赛中从山坡上的点O打出一球向球洞A飞去,球的飞行路线为抛物线,如果不考虑空气阻力,当球达到最大铅垂高度12m时,球移动的水平距离为9m.已知山坡OA与水平方向OC的夹角为30°,O,A两点相距8$\sqrt{3}$ m.
如图,小明在一次高尔夫球争霸赛中从山坡上的点O打出一球向球洞A飞去,球的飞行路线为抛物线,如果不考虑空气阻力,当球达到最大铅垂高度12m时,球移动的水平距离为9m.已知山坡OA与水平方向OC的夹角为30°,O,A两点相距8$\sqrt{3}$ m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
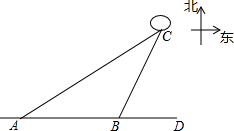 一条船从海岛A出发,以25海里/时的速度向正东方向航行,2小时后到达海岛B处,从A、B望灯塔C,测得∠DBC=68°,∠DAC=34°,求海岛B与灯塔C的距离.
一条船从海岛A出发,以25海里/时的速度向正东方向航行,2小时后到达海岛B处,从A、B望灯塔C,测得∠DBC=68°,∠DAC=34°,求海岛B与灯塔C的距离.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com