
【题目】如图,在Rt![]() 中,
中,![]() ,点
,点![]() 为
为![]() 边上一个动点,过点
边上一个动点,过点![]() 作
作![]() 交边
交边![]() 于
于![]() ,过点
,过点![]() 作射线
作射线![]() 交
交![]() 边于点
边于点![]() ,交射线
,交射线![]() 于点
于点![]() ,联结
,联结![]() .设
.设![]() 两点的距离为
两点的距离为![]() ,
,![]() 两点的距离为
两点的距离为![]() .
.
(1)求证:![]() ;
;
(2)求![]() 关于
关于![]() 的函数解析式,并写出
的函数解析式,并写出![]() 的取值范围;
的取值范围;
(3)点![]() 在运动过程中,
在运动过程中,![]() 能否构成等腰三角形?如果能,请直接写出
能否构成等腰三角形?如果能,请直接写出![]() 的长,如果不能,请简要说明理由.
的长,如果不能,请简要说明理由.
【答案】(1)见解析;(2)y=2x-6(3≤x≤12);(3)能,3或6![]() -6或6
-6或6
【解析】
(1)根据三角形的内角和定理先得∠B=60°,证明△BED是等边三角形,根据等角对等边分别证明DE=DG,BD=ED,可得结论;
(2)先得BC=6,根据直角三角形30度角的性质可得结论;
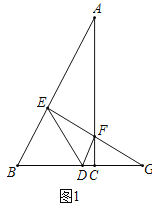
(3)分三种情况:①当ED=DF时,当F与C重合时,如图2,BE=![]() BC=3;②当ED=EF时,如图3,根据直角三角形30度角的性质或三角函数列等式可得结论;③当EF=DF时,C与D重合,如图4,此时BE=BC=6;
BC=3;②当ED=EF时,如图3,根据直角三角形30度角的性质或三角函数列等式可得结论;③当EF=DF时,C与D重合,如图4,此时BE=BC=6;
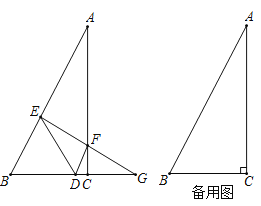
(1)证明:如图1,
Rt△ABC中,∠A=30°,∠C=90°,
∴∠B=60°,
∵∠BDE=∠B=60°,
∴∠BED=60°,
∴△BED是等边三角形,
∴BD=ED,
∵EF⊥AB,
∴∠BEF=90°,
∴∠DEG=30°,
∵∠EDB=∠DEG+∠DGE,
∴∠DGE=60°-30°=30°=∠DEF,
∴DE=DG,
∴BD=DG;
(2)解:如图1,Rt△ABC中,∠A=30°,∠C=90°,AB=12,
∴BC=6,
Rt△BEG中,∠G=30°,
∴BG=2BE,
∵BE两点的距离为x,CG两点的距离为y,
∴6+y=2x,y=2x-6(3≤x≤12);
(3)解:分三种情况:
①当ED=DF时,当F与C重合时,如图2,BE=![]() BC=3;
BC=3;
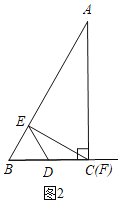
②当ED=EF时,如图3,
BE=ED=EF=x,
∴AE=12-x,
Rt△AEF中,tan∠A=![]() ,
,
∵∠A=30°,
∴![]() ,
,
∴x=6![]() -6,
-6,
∴BE=6![]() -6;
-6;
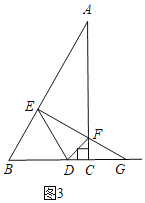
③当EF=DF时,C与D重合,如图4,此时BE=BC=6;
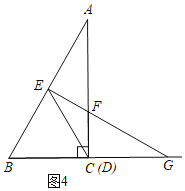
综上,当△DEF构成等腰三角形时,BE的长为3或6![]() -6或6,
-6或6,


科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,∠BAC>90°,点D为BC的中点,点E在AC上,将△CDE沿DE折叠,使得点C恰好落在BA的延长线上的点F处,连结AD,则下列结论不一定正确的是( )

A. AE=EF B. AB=2DE
C. △ADF和△ADE的面积相等 D. △ADE和△FDE的面积相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从甲、乙两位运动员中选出一名参加在规定时间内的投篮比赛.预先对这两名运动员进行了6次测试,成绩如下(单位:个):
甲:6,12,8,12,10,12;
乙:9,10,11,10,12,8;
(1)填表:
平均数 | 众数 | 方差 | |
甲 | 10 |
|
|
乙 |
| 10 |
|
(2)根据测试成绩,请你运用所学的统计知识作出分析,派哪一位运动员参赛更好?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,平面直角坐标系中,B、C两点的坐标分别为B(0,3)和C(0,﹣![]() ),点A在x轴正半轴上,且满足∠BAO=30°.
),点A在x轴正半轴上,且满足∠BAO=30°.
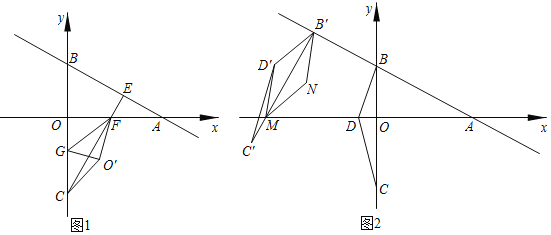
(1)过点C作CE⊥AB于点E,交AO于点F,点G为线段OC上一动点,连接GF,将△OFG沿FG翻折使点O落在平面内的点O′处,连接O′C,求线段OF的长以及线段O′C的最小值;
(2)如图2,点D的坐标为D(﹣1,0),将△BDC绕点B顺时针旋转,使得BC⊥AB于点B,将旋转后的△BDC沿直线AB平移,平移中的△BDC记为△B′D′C′,设直线B′C′与x轴交于点M,N为平面内任意一点,当以B′、D′、M、N为顶点的四边形是菱形时,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
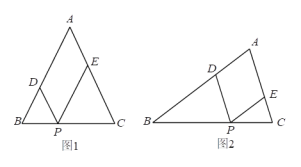
【题目】如图1,△ABC为等腰三角形,AB=AC=a,P点是底边BC上的一个动点,PD∥AC,PE∥AB.
⑴用a表示四边形ADPE的周长为 ;
⑵点P运动到什么位置时,四边形ADPE是菱形,请说明理由;
⑶如果△ABC不是等腰三角形(图2),其他条件不变,点P运动到什么位置时,四边形ADPE是菱形(不必说明理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经市场调查,某种商品在第x天的售价与销量的相关信息如下表;已知该商品的进价为每件30元,设销售该商品每天的利润为y元.

(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
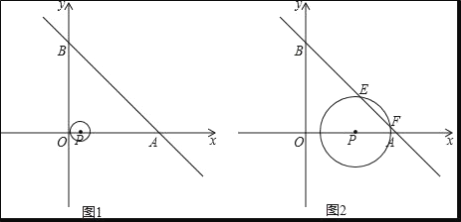
【题目】如图1,一次函数y=﹣x+10的图象交x轴于点A,交y轴于点B.以P(1,0)为圆心的⊙P与y轴相切,若点P以每秒2个单位的速度沿x轴向右平移,同时⊙P的半径以每秒增加1个单位的速度不断变大,设运动时间为t(s)
(1)点A的坐标为 ,点B的坐标为 ,∠OAB= °;
(2)在运动过程中,点P的坐标为 ,⊙P的半径为 (用含t的代数式表示);
(3)当⊙P与直线AB相交于点E、F时
①如图2,求t=![]() 时,弦EF的长;
时,弦EF的长;
②在运动过程中,是否存在以点P为直角顶点的Rt△PEF,若存在,请求出t的值;若不存在,请说明理由(利用图1解题).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年中秋节来期间,某超市以每盒80元的价格购进了1000盒月饼,第一周以每盒168元的价格销售了300盒,第二周如果单价不变,预计仍可售出300盒,该超市经理为了增加销量,决定降价,据调查,单价每降低1元,可多售出10盒,但最低每盒要赢利30元,第二周结束后,该超市将对剩余的月饼一次性赔钱甩卖,此时价格为70元/盒.
(1)若设第二周单价降低x元,则第二周的单价是 ______ ,销量是 ______ ;
(2)经两周后还剩余月饼 ______ 盒;
(3)若该超市想通过销售这批月饼获利51360元,那么第二周的单价应是多元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com