
分析 过A,C作AE,CF垂直于L2,点E,F是垂足,将Rt△BCF绕点B逆时针旋转60°至Rt△BAD处,延长DA交L2于点G,首先可求出BD的长,在Rt△ABD中,再根据勾股定理即可求出AB的长.
解答 解:如图所示,过A,C作AE,CF垂直于L2,点E,F是垂足,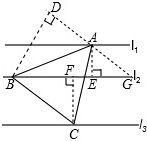 将Rt△BCF绕点B逆时针旋转60°至Rt△BAD处,延长DA交L2于点G,
将Rt△BCF绕点B逆时针旋转60°至Rt△BAD处,延长DA交L2于点G,
由作图可知:∠DBG=60°,AD=CF=2.
在Rt△BDG中,∠BGD=30°.在Rt△AEG中,∠EAG=60°,AE=1,AG=2,DG=4.
∴BD=$\frac{4\sqrt{3}}{3}$.
在Rt△ABD中,AB=$\sqrt{B{D}^{2}+A{D}^{2}}$=$\frac{2\sqrt{21}}{3}$,
故答案为:$\frac{2\sqrt{21}}{3}$.
点评 本题考查了勾股定理,此题比较复杂,结合了平行线的性质,等腰三角形,直角三角形的性质,是一道具有一定综合性的好题.


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
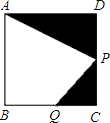 已知如图,正方形ABCD的边长为1,P是CD边的中点,点Q在线段BC上,设BQ=k,是否存在这样的实数k,使得Q、C、P为顶点的三角形与△ADP相似?若存在,求出k的值;若不存在,请说明理由.
已知如图,正方形ABCD的边长为1,P是CD边的中点,点Q在线段BC上,设BQ=k,是否存在这样的实数k,使得Q、C、P为顶点的三角形与△ADP相似?若存在,求出k的值;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 运输单位 | 运输速度 (千米/时) | 运费单价 元/(吨•千米) | 运输途中冷藏 元/(吨•时) | 装卸总费用(元) |
| 汽车货运公司 | 75 | 1.5 | 5 | 4000 |
| 火车货运站 | 100 | 1.3 | 5 | 6600 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k>0,b>0 | B. | k>0,b<0 | C. | k<0,b<0 | D. | k<0,b>0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com